"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ РЯД
Значение ФУРЬЕ РЯД в математической энциклопедии:
функции f(х)по ортонормированной на промежутке ( а, b )системе функций  -ряд
-ряд

коэффициенты к-рого определяются по формулам

и наз. коэффициентами Фурье функции f. О функции f в общем случае предполагается, что она интегрируема с квадратом на ( а, b). Для многих систем  это требование можно ослабить, заменив его каким-либо другим, обеспечивающим существование всех интегралов (1).
это требование можно ослабить, заменив его каким-либо другим, обеспечивающим существование всех интегралов (1).
По тригонометрич. системе Ф. р. определяется для каждой функции f, интегрируемой на  Это ряд
Это ряд

с коэффициентами

Аналогично строятся Ф. р. для функций от многих переменных. Дальнейшие обобщения приводят к коэффициентам Фурье и Ф. р. элементов гильбертова пространства.
Наиболее глубоко разработана теория Ф. р. по тригонометрич. системе, к-рые были первыми примерами Ф. р. Имея в виду Ф. р. по тригонометрич. системе, обычно говорят просто о Ф. р., не указывая, но какой системе они строятся.
Ф. р. составляют значительную часть теории тригонометрических рядов. Впервые Ф. р. появились в работах Ж. Фурье (J. Fourier, 1807), посвященных исследованию задач теплопроводности. Он предложил для представления функции f, заданной на  тригонометрич. рядом брать ряд (2) с коэффициентами, определяемыми по формулам (3). Такой выбор коэффициентов является естественным со многих точек зрения. Напр., если ряд (2) сходится к функции f(x)равномерно, то почленное интегрирование приводит к выражению коэффициентов а k и bk по формулам (3). С помощью почленного интегрирования эти формулы получал еще Л. Эйлер (L. Euler, 1777).
тригонометрич. рядом брать ряд (2) с коэффициентами, определяемыми по формулам (3). Такой выбор коэффициентов является естественным со многих точек зрения. Напр., если ряд (2) сходится к функции f(x)равномерно, то почленное интегрирование приводит к выражению коэффициентов а k и bk по формулам (3). С помощью почленного интегрирования эти формулы получал еще Л. Эйлер (L. Euler, 1777).
С помощью формул (3) Ф. р. (2) строится для каждой функции, интегрируемой на  Интегрируемость функции может пониматься по-разному, напр. как интегрируемость по Риману или но Лебегу. В зависимости от этого говорят о рядах Фурье-Римана, Фурье - Лебега и т. п. Сами понятия интегралов Римана и Лебега возникли в значительной степени в связи с исследованиями Ф. р. Современный вид теория Ф. р. приобрела после построения интеграла Лебега, после чего она развивается главным образом как теория рядов Фурье-Лебега. Ниже о функции f предполагается, что она имеет период
Интегрируемость функции может пониматься по-разному, напр. как интегрируемость по Риману или но Лебегу. В зависимости от этого говорят о рядах Фурье-Римана, Фурье - Лебега и т. п. Сами понятия интегралов Римана и Лебега возникли в значительной степени в связи с исследованиями Ф. р. Современный вид теория Ф. р. приобрела после построения интеграла Лебега, после чего она развивается главным образом как теория рядов Фурье-Лебега. Ниже о функции f предполагается, что она имеет период  и интегрируема по Лебегу на периоде.
и интегрируема по Лебегу на периоде.
В теории Ф. р. изучается связь свойств функций со свойствами их Ф. р., в частности исследуются вопросы представления функций с помощью Ф. р.
К работе Ф. Бесселя (F. Bessel, 1828) восходит доказательство минимального свойства частных сумм Ф. р.: для функций  среди тригонометрич. полиномов порядка n
среди тригонометрич. полиномов порядка n

наименьшее значение интегралу

доставляет частная сумма Ф. р. (2) функции f:
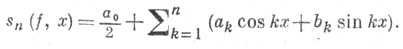
Это наименьшее значение равно

Отсюда следует Бесселя неравенство

выполняющееся для каждой функции f из L2.
Система тригонометрич. функций является замкнутой системой, т. е. если  то справедливо Парсеваля равенство
то справедливо Парсеваля равенство

где а k, bk- коэффициенты Фурье функции f. В частности, для функций f из L2 сходится ряд

Имеет место и обратное утверждение: если для системы чисел а k, bk ряд (4) сходится, то эти числа являются коэффициентами Фурье нек-рой функции  [Ф. Рисc (F. Biesz), Э. Фишер (Е. Fischer), 1907].
[Ф. Рисc (F. Biesz), Э. Фишер (Е. Fischer), 1907].
Коэффициенты Фурье каждой интегрируемой функции стремятся к нулю. Эту теорему наз. теоремой Римана - Лебега. Б. Риман (В. Riemann) доказал ее для рядов Фурье-Римана, А. Лебег (Н. Lebesgue) - для рядов Фурье-Лебега.
Если функция f абсолютно непрерывна, то Ф. р. производной f' можно получить почленным дифференцированием Ф. р. функции f. Отсюда следует, что если производная порядка  функции f абсолютно непрерывна, то для коэффициентов Фурье функции f справедлива оценка
функции f абсолютно непрерывна, то для коэффициентов Фурье функции f справедлива оценка

Первый признак сходимости Ф. р. получил П. Дирихле (P. Dirichlet, 1829). Его результат (Дирихле теорема )можно сформулировать так: если функция f имеет на периоде конечное число максимумов и минимумов и непрерывна всюду, кроме конечного числа точек, в к-рых она может иметь разрывы 1-го рода, то Ф. р. функции f сходится для всех х, причем в точках непрерывности он сходится к f(x). а в точках разрыва к  В дальнейшем это утверждение было распространено на произвольные функции ограниченной вариации [К. Жордан (С. Jordan), 1881].
В дальнейшем это утверждение было распространено на произвольные функции ограниченной вариации [К. Жордан (С. Jordan), 1881].
Согласно принципу локализации, доказанному Б. Риманом (1853), сходимость или расходимость Ф. р. функции f в точке хи значение суммы в случае сходимости зависят только от поведения функции f в как угодно малой окрестности точки х.
Известно много разных признаков сходимости Ф. р. в точке. Р. Липшиц (R. Lipschitz, 1864) установил, что Ф. р. функции f сходится в точке х, если для достаточно малых hвыполнено условие  где М и
где М и  - нек-рые положительные постоянные. Более общим является Дани признак: Ф. р. функции f сходится в точке хк числу S, если сходится интеграл
- нек-рые положительные постоянные. Более общим является Дани признак: Ф. р. функции f сходится в точке хк числу S, если сходится интеграл

где  В качестве числа Sобычно выступает значение f(x). Напр., если Ф. р. функции f сходится в точке х, в к-рой эта функция непрерывна, то сумма ряда обязательно равна f(x).
В качестве числа Sобычно выступает значение f(x). Напр., если Ф. р. функции f сходится в точке х, в к-рой эта функция непрерывна, то сумма ряда обязательно равна f(x).
А. Лебег (1905) доказал, что если при  справедливы оценки
справедливы оценки

то Ф. р. функции f сходится в точке хк числу S. Этот Лебега признак сильнее как всех приведенных вышше, так и Валле Пуссена признака и Юнга признака. Но проверка его обычно затруднительна. Признак сходимости другого типа дает теорема Харди - Литлвуда (1932): Ф. р. функции f сходится в точке х, если выполнены следующие условия:
1) при 

2) для коэффициентов Фурье функции f справедливы оценки

Наряду с признаками сходимости Ф. р. в точке, изучаются признаки равномерной сходимости. Пусть функция f имеет период  и непрерывна. Тогда ее Ф. р. сходится к ней равномерно на всей числовой оси, если
и непрерывна. Тогда ее Ф. р. сходится к ней равномерно на всей числовой оси, если  - непрерывности модуль функции f- удовлетворяет условию
- непрерывности модуль функции f- удовлетворяет условию
 при
при  ( Дини-Липшица признак )или если f имеет ограниченную вариацию (Жордана признак).
( Дини-Липшица признак )или если f имеет ограниченную вариацию (Жордана признак).
Отсюда можно получать признаки равномерной сходимости Ф. р. на нек-ром отрезке, если воспользоваться принципом локализации для равномерной сходимости, к-рый формулируется так. Если две функции равны на отрезке [а, b], то на каждом строго внутреннем к нему отрезке  Ф. р. этих функций или оба равномерно сходятся или оба не являются равномерно сходящимися. Другими словами, равномерная сходимость Ф. р. функции f на отрезке зависит только от поведения функции f в произвольно малом расширении этого отрезка.
Ф. р. этих функций или оба равномерно сходятся или оба не являются равномерно сходящимися. Другими словами, равномерная сходимость Ф. р. функции f на отрезке зависит только от поведения функции f в произвольно малом расширении этого отрезка.
П. Дюбуа-Реймон (P. Du Bois Reymond, 1873) установил, что непрерывность функции в нек-рой точке не гарантирует сходимость ее Ф. р. в этой точке, В дальнейшем было доказано, что Ф. р. непрерывной функции может расходиться на всюду плотном множестве точек меры нуль, имеющем вторую категорию.
Если о функции не предполагать ничего, кроме интегрируемости, то ее Ф. р. может оказаться расходящимся почти всюду или даже всюду. Первые примеры таких функций построил А. Н. Колмогоров (1923). Позднее было выяснено, что этим свойством могут обладать Ф. р. и самой функции и функции, сопряженной с ней.
Еще в 1915 Н. Н. Лузин высказал гипотезу, что Ф. р. каждой функции из L2 сходится почти всюду. Долгое время в этом направлении получали лить частные результаты. В общем виде задача оказалась очень трудной и только в 1966 Л. Карлесон (L. Carleson) доказал справедливость этой гипотезы (см. Карлесона теорема). Ф. р. функций из Lp при р>1 также сходятся почти всюду. Пример Колмогорова показывает, что дальнейшее усиление этого результата в терминах пространств LP невозможно.
Поскольку частные суммы Ф. р. не всегда сходятся, рассматривается суммирование рядов Фурье, когда для представления функции используются те или иные средние частных сумм ее Ф. р. Один из наиболее простых примеров - Фейера суммы, являющиеся средними арифметическими частных сумм Ф. p. sk(f, х),

Для каждой интегрируемой функции f суммы  сходятся к f(x)почти всюду, при этом сходятся в каждой точке непрерывности f, а если f непрерывна всюду, то сходятся равномерно.
сходятся к f(x)почти всюду, при этом сходятся в каждой точке непрерывности f, а если f непрерывна всюду, то сходятся равномерно.
Согласно Данжуа-Лузина теореме, если тригонометрич. ряд (2) сходится абсолютно на множестве положительной меры, то сходится ряд

и, значит, ряд (2) абсолютно сходится для всех х. Таким образом, абсолютная сходимость ряда (2) эквивалентна сходимости ряда (5).
С. Н. Бернштейн (1934) доказал, что если модуль непрерывности  функции f удовлетворяет условию
функции f удовлетворяет условию

то Ф. р. функции f сходится абсолютно. Это условие нельзя ослабить: если функция типа модуля непрерывности  такова, что ряд
такова, что ряд

расходится, то найдется функция f, для модуля непрерывности к-рой выполняется оценка  а ее Ф. р. не сходится абсолютно. В частности, абсолютно сходятся Ф. р. функций, удовлетворяющих Липшица условию порядка
а ее Ф. р. не сходится абсолютно. В частности, абсолютно сходятся Ф. р. функций, удовлетворяющих Липшица условию порядка 
А при  абсолютной сходимости может не быть (С. Н. Бернштейн, 1914).
абсолютной сходимости может не быть (С. Н. Бернштейн, 1914).
Если функция f имеет ограниченную вариацию и ее модуль непрерывности удовлетворяет условию

то Ф. р. функции f сходится абсолютно (см. [9]). Условие (6) ослабить нельзя (см. [10]).
В отличие от предыдущих следующая теорема дает критерий абсолютной сходимости для индивидуальной функции. Для абсолютной сходимости Ф. р. функции необходима и достаточна сходимость ряда

где е п(f)- наилучшее приближение функции f в метрике пространства L2 трпгонометрич. полиномами, содержащими и гармоник (см. [11]).
Ряд (2) можно рассматривать как действительную часть степенного ряда

Мнимую часть

наз. рядом, сопряженным с рядом (2).
Пусть  и (2) - ее Ф. р. Тогда для почти всех хсуществует функция
и (2) - ее Ф. р. Тогда для почти всех хсуществует функция

(И. И. Привалов, 1919). Функцию  наз. сопряженной с f, она может быть неинтегрируемой. Но если
наз. сопряженной с f, она может быть неинтегрируемой. Но если  то Ф. р. функции
то Ф. р. функции  является ряд (7) (В. И. Смирнов, 1928).
является ряд (7) (В. И. Смирнов, 1928).
Во многих случаях по свойствам функции f или ее Ф. р. (2) удается установить те или иные свойства сопряженного ряда (7), напр. его сходимость в метрике Lp, сходимость или суммируемость в точке, почти всюду и т. п.
Изучаются также свойства Ф. р. при специальных предположениях об их коэффициентах. Напр., лакунарные тригонометрические ряды, когда отличны от нуля только коэффициенты с номерами п т, образующими лакунарную последовательность, т. е. такими, что  Другой пример специальных рядов - ряды с монотонными коэффициентами.
Другой пример специальных рядов - ряды с монотонными коэффициентами.
Все сказанное выше относилось к Ф. р. вида (2). Для Ф. р. по переставленной тригонометрич. системе нек-рые свойства Ф. р. по тригонометрич. системе, взятой в обычном порядке, не имеют места. Напр., существует такая непрерывная функция, что ее Ф. р. после нек-poй перестановки расходится почти всюду (см. [12] - [15]).
Теория Ф. р. для функций многих переменных разработана в меньшей степени. Часть многомерных результатов аналогична одномерным. Но имеются и существенные отличия.
Пусть x=(x1, ..., х N )-точка N-мерного пространства, k= (k1,..., kN) есть N-мерный вектор с целочисленными координатами и (k, х)= klxl+ .... + kNxpN. Для функции f(х), имеющей период  по каждой переменной и интегрируемой по Лебегу на N-мерном кубе
по каждой переменной и интегрируемой по Лебегу на N-мерном кубе  Ф. р. по тригонометрич. системе наз. ряд
Ф. р. по тригонометрич. системе наз. ряд

где суммирование ведется по всем . и

- коэффициенты Фурье функции f. Ф. р. (8) записан в комплексной форме. Запись его в тригонометрич. форме как ряда по произведениям косинусов и синусов кратных дуг более громоздка.
Возможны различные определения частных сумм ряда (8), напр. частные суммы по прямоугольникам

по кругам

где n -радиус и 
Для представления функций круговые частные суммы (9) менее пригодны, чем их средние Рисса

Для средних Рисса порядка  Ф. р. функций из L2 справедлив принцип локализации, а для меньших
Ф. р. функций из L2 справедлив принцип локализации, а для меньших  это не так (С. Бохнер, S. Bochrier, 1936). Средние Рисса круговых частных сумм критич. порядка
это не так (С. Бохнер, S. Bochrier, 1936). Средние Рисса круговых частных сумм критич. порядка  играют существенную роль и в других вопросах Ф. р. функций многих неременных.
играют существенную роль и в других вопросах Ф. р. функций многих неременных.
Существует непрерывная функция двух переменных, Ф. р. к-рой не сходится по прямоугольникам ни в одной внутренней точке квадрата  (см. [16]).
(см. [16]).
Нек-рые результаты, относящиеся к Ф. р. по триго-нометрич. системе, допускают значительные обобщения, напр. могут быть соответствующим образом перенесены на спектральные разложения, отвечающие самосопряженным эллиптическим дифференциальным операторам.
Лит.:[1] Б а р и Н. К., Тригонометрические ряды, М., 1961; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., 2 изд., т. 1-2, М., 1965; [3] Xарди Г. X., Рогозинский В. В., Ряды Фурье, пер. с англ., М., 1959; [4] Лузин Н. Н., Интеграл и тригонометрический ряд, М.- Л., 1951; [5] Lebesgue Н., Lemons sur les series trigonometriques, P., 1906; [6] Паплаускас А. Б., Тригонометрические ряды от Эйлера до Лебега, М., 1966; [7] Ульянов П. Л., лУспехи матем. наук

 -ряд
-ряд 

 это требование можно ослабить, заменив его каким-либо другим, обеспечивающим существование всех интегралов (1).
это требование можно ослабить, заменив его каким-либо другим, обеспечивающим существование всех интегралов (1).  Это ряд
Это ряд 

 тригонометрич. рядом брать ряд (2) с коэффициентами, определяемыми по формулам (3). Такой выбор коэффициентов является естественным со многих точек зрения. Напр., если ряд (2) сходится к функции f(x)равномерно, то почленное интегрирование приводит к выражению коэффициентов а k и bk по формулам (3). С помощью почленного интегрирования эти формулы получал еще Л. Эйлер (L. Euler, 1777).
тригонометрич. рядом брать ряд (2) с коэффициентами, определяемыми по формулам (3). Такой выбор коэффициентов является естественным со многих точек зрения. Напр., если ряд (2) сходится к функции f(x)равномерно, то почленное интегрирование приводит к выражению коэффициентов а k и bk по формулам (3). С помощью почленного интегрирования эти формулы получал еще Л. Эйлер (L. Euler, 1777).  Интегрируемость функции может пониматься по-разному, напр. как интегрируемость по Риману или но Лебегу. В зависимости от этого говорят о рядах Фурье-Римана, Фурье - Лебега и т. п. Сами понятия интегралов Римана и Лебега возникли в значительной степени в связи с исследованиями Ф. р. Современный вид теория Ф. р. приобрела после построения интеграла Лебега, после чего она развивается главным образом как теория рядов Фурье-Лебега. Ниже о функции f предполагается, что она имеет период
Интегрируемость функции может пониматься по-разному, напр. как интегрируемость по Риману или но Лебегу. В зависимости от этого говорят о рядах Фурье-Римана, Фурье - Лебега и т. п. Сами понятия интегралов Римана и Лебега возникли в значительной степени в связи с исследованиями Ф. р. Современный вид теория Ф. р. приобрела после построения интеграла Лебега, после чего она развивается главным образом как теория рядов Фурье-Лебега. Ниже о функции f предполагается, что она имеет период  и интегрируема по Лебегу на периоде.
и интегрируема по Лебегу на периоде.  среди тригонометрич. полиномов порядка n
среди тригонометрич. полиномов порядка n 

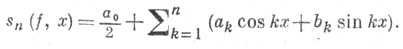


 то справедливо Парсеваля равенство
то справедливо Парсеваля равенство 

 [Ф. Рисc (F. Biesz), Э. Фишер (Е. Fischer), 1907].
[Ф. Рисc (F. Biesz), Э. Фишер (Е. Fischer), 1907].  функции f абсолютно непрерывна, то для коэффициентов Фурье функции f справедлива оценка
функции f абсолютно непрерывна, то для коэффициентов Фурье функции f справедлива оценка 
 В дальнейшем это утверждение было распространено на произвольные функции ограниченной вариации [К. Жордан (С. Jordan), 1881].
В дальнейшем это утверждение было распространено на произвольные функции ограниченной вариации [К. Жордан (С. Jordan), 1881].  где М и
где М и  - нек-рые положительные постоянные. Более общим является Дани признак: Ф. р. функции f сходится в точке хк числу S, если сходится интеграл
- нек-рые положительные постоянные. Более общим является Дани признак: Ф. р. функции f сходится в точке хк числу S, если сходится интеграл 
 В качестве числа Sобычно выступает значение f(x). Напр., если Ф. р. функции f сходится в точке х, в к-рой эта функция непрерывна, то сумма ряда обязательно равна f(x).
В качестве числа Sобычно выступает значение f(x). Напр., если Ф. р. функции f сходится в точке х, в к-рой эта функция непрерывна, то сумма ряда обязательно равна f(x).  справедливы оценки
справедливы оценки 



 и непрерывна. Тогда ее Ф. р. сходится к ней равномерно на всей числовой оси, если
и непрерывна. Тогда ее Ф. р. сходится к ней равномерно на всей числовой оси, если  - непрерывности модуль функции f- удовлетворяет условию
- непрерывности модуль функции f- удовлетворяет условию  при
при  ( Дини-Липшица признак )или если f имеет ограниченную вариацию (Жордана признак).
( Дини-Липшица признак )или если f имеет ограниченную вариацию (Жордана признак).  Ф. р. этих функций или оба равномерно сходятся или оба не являются равномерно сходящимися. Другими словами, равномерная сходимость Ф. р. функции f на отрезке зависит только от поведения функции f в произвольно малом расширении этого отрезка.
Ф. р. этих функций или оба равномерно сходятся или оба не являются равномерно сходящимися. Другими словами, равномерная сходимость Ф. р. функции f на отрезке зависит только от поведения функции f в произвольно малом расширении этого отрезка. 
 сходятся к f(x)почти всюду, при этом сходятся в каждой точке непрерывности f, а если f непрерывна всюду, то сходятся равномерно.
сходятся к f(x)почти всюду, при этом сходятся в каждой точке непрерывности f, а если f непрерывна всюду, то сходятся равномерно. 
 функции f удовлетворяет условию
функции f удовлетворяет условию 
 такова, что ряд
такова, что ряд 
 а ее Ф. р. не сходится абсолютно. В частности, абсолютно сходятся Ф. р. функций, удовлетворяющих Липшица условию порядка
а ее Ф. р. не сходится абсолютно. В частности, абсолютно сходятся Ф. р. функций, удовлетворяющих Липшица условию порядка 
 абсолютной сходимости может не быть (С. Н. Бернштейн, 1914).
абсолютной сходимости может не быть (С. Н. Бернштейн, 1914). 



 и (2) - ее Ф. р. Тогда для почти всех хсуществует функция
и (2) - ее Ф. р. Тогда для почти всех хсуществует функция 
 наз. сопряженной с f, она может быть неинтегрируемой. Но если
наз. сопряженной с f, она может быть неинтегрируемой. Но если  то Ф. р. функции
то Ф. р. функции  является ряд (7) (В. И. Смирнов, 1928).
является ряд (7) (В. И. Смирнов, 1928).  Другой пример специальных рядов - ряды с монотонными коэффициентами.
Другой пример специальных рядов - ряды с монотонными коэффициентами.  по каждой переменной и интегрируемой по Лебегу на N-мерном кубе
по каждой переменной и интегрируемой по Лебегу на N-мерном кубе  Ф. р. по тригонометрич. системе наз. ряд
Ф. р. по тригонометрич. системе наз. ряд 





 Ф. р. функций из L2 справедлив принцип локализации, а для меньших
Ф. р. функций из L2 справедлив принцип локализации, а для меньших  это не так (С. Бохнер, S. Bochrier, 1936). Средние Рисса круговых частных сумм критич. порядка
это не так (С. Бохнер, S. Bochrier, 1936). Средние Рисса круговых частных сумм критич. порядка  играют существенную роль и в других вопросах Ф. р. функций многих неременных.
играют существенную роль и в других вопросах Ф. р. функций многих неременных.  (см. [16]).
(см. [16]).