"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ ПРЕОБРАЗОВАНИЕ ДИСКРЕТНОЕЗначение ФУРЬЕ ПРЕОБРАЗОВАНИЕ ДИСКРЕТНОЕ в математической энциклопедии:
-преобразование, используемое для гармонич. анализа функций, заданных на дискретном множестве точек.
Если на множестве точек  функция задана своими значениями функция задана своими значениями  Т> 0 - период функции, то Ф. п. д. вектора х= (х 0, x1, ..., xN-1) есть вектор Т> 0 - период функции, то Ф. п. д. вектора х= (х 0, x1, ..., xN-1) есть вектор  где F- матрица с элементами где F- матрица с элементами  i - мнимая единица, i - мнимая единица, 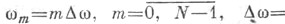  Компоненты вектора Компоненты вектора  аналогичны коэффициентам Фурье в обычных тригонометрич. разложениях. Ф. п. д. используется для приближенного вычисления этих коэффициентов, спектров, авто- и взаимно корреляционных функций и т. п. Прямое вычисление Ф. п. д. требует выполнения около N2 арифметич. операций и большой затраты машинного времени. Метод быстрого преобразования Фурье (см. [1]) позволил существенно сократить число операций. При N=n1 n2. . . п т этот метод выполняет Ф. п. д. приблизительно за N(п 1+п2+. . .+п т )операций, повышая точность вычислений. Особенно удобные для реализации алгоритмы получаются при N=2m. Имеется значительное число программ, реализующих или использующих быстрое преобразование Фурье для решения прикладных задач. Метод быстрого преобразования Фурье включает в себя широко известные экономичные способы вычисления Ф. п. д., напр. метод Рунге (см. [2]). аналогичны коэффициентам Фурье в обычных тригонометрич. разложениях. Ф. п. д. используется для приближенного вычисления этих коэффициентов, спектров, авто- и взаимно корреляционных функций и т. п. Прямое вычисление Ф. п. д. требует выполнения около N2 арифметич. операций и большой затраты машинного времени. Метод быстрого преобразования Фурье (см. [1]) позволил существенно сократить число операций. При N=n1 n2. . . п т этот метод выполняет Ф. п. д. приблизительно за N(п 1+п2+. . .+п т )операций, повышая точность вычислений. Особенно удобные для реализации алгоритмы получаются при N=2m. Имеется значительное число программ, реализующих или использующих быстрое преобразование Фурье для решения прикладных задач. Метод быстрого преобразования Фурье включает в себя широко известные экономичные способы вычисления Ф. п. д., напр. метод Рунге (см. [2]). Лит.:[1] Сoolеу J., Тukеу J., лMath. Comput.
|

 функция задана своими значениями
функция задана своими значениями  Т> 0 - период функции, то Ф. п. д. вектора х= (х 0, x1, ..., xN-1) есть вектор
Т> 0 - период функции, то Ф. п. д. вектора х= (х 0, x1, ..., xN-1) есть вектор  где F- матрица с элементами
где F- матрица с элементами  i - мнимая единица,
i - мнимая единица, 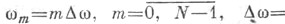
 Компоненты вектора
Компоненты вектора  аналогичны коэффициентам Фурье в обычных тригонометрич. разложениях. Ф. п. д. используется для приближенного вычисления этих коэффициентов, спектров, авто- и взаимно корреляционных функций и т. п. Прямое вычисление Ф. п. д. требует выполнения около N2 арифметич. операций и большой затраты машинного времени. Метод быстрого преобразования Фурье (см. [1]) позволил существенно сократить число операций. При N=n1 n2. . . п т этот метод выполняет Ф. п. д. приблизительно за N(п 1+п2+. . .+п т )операций, повышая точность вычислений. Особенно удобные для реализации алгоритмы получаются при N=2m. Имеется значительное число программ, реализующих или использующих быстрое преобразование Фурье для решения прикладных задач. Метод быстрого преобразования Фурье включает в себя широко известные экономичные способы вычисления Ф. п. д., напр. метод Рунге (см. [2]).
аналогичны коэффициентам Фурье в обычных тригонометрич. разложениях. Ф. п. д. используется для приближенного вычисления этих коэффициентов, спектров, авто- и взаимно корреляционных функций и т. п. Прямое вычисление Ф. п. д. требует выполнения около N2 арифметич. операций и большой затраты машинного времени. Метод быстрого преобразования Фурье (см. [1]) позволил существенно сократить число операций. При N=n1 n2. . . п т этот метод выполняет Ф. п. д. приблизительно за N(п 1+п2+. . .+п т )операций, повышая точность вычислений. Особенно удобные для реализации алгоритмы получаются при N=2m. Имеется значительное число программ, реализующих или использующих быстрое преобразование Фурье для решения прикладных задач. Метод быстрого преобразования Фурье включает в себя широко известные экономичные способы вычисления Ф. п. д., напр. метод Рунге (см. [2]).