"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ ПРЕОБРАЗОВАНИЕ
Значение ФУРЬЕ ПРЕОБРАЗОВАНИЕ в математической энциклопедии:
обобщенной функции - расширение операции преобразования Фурье с основных функций на обобщенные функции. Пусть К - пространство основных функций, на к-ром определена операция преобразования Фурье F,

причем F- изоморфизм Кна пространство основных функций 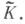 Тогда операция преобразования Фурье
Тогда операция преобразования Фурье  определяемая на пространстве обобщенных функций
определяемая на пространстве обобщенных функций  равенством
равенством
 осуществляет изоморфизм
осуществляет изоморфизм  на пространство основных функций К'.
на пространство основных функций К'.
Примеры. 1)  Здесь обратной операцией к Fслужит операция
Здесь обратной операцией к Fслужит операция

и справедливы основные формулы для 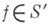
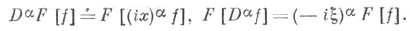
2)  где
где  -совокупность функций
-совокупность функций  таких, что
таких, что 
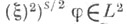 и
и 
3) K = D,  где Z - совокупность целых функций
где Z - совокупность целых функций  удовлетворяющих условию роста; существует число
удовлетворяющих условию роста; существует число 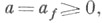 что для любого
что для любого 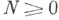 найдется С N > 0 такое, что
найдется С N > 0 такое, что

Ряды Фурье обобщенной функции. Если обобщенная функция f-периодическая с n-периодом Т = (Т 1, ..., Т п), Tj> 0, то  и ее можно разложить в тригонометрич. ряд
и ее можно разложить в тригонометрич. ряд
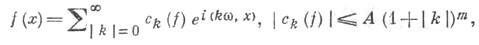
сходящийся к f в S'; здесь
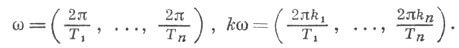
Примеры. 4) 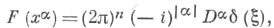 в частности
в частности 
5)  в частности
в частности 
6) 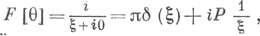 где
где  -функция Хeвисайда.
-функция Хeвисайда.
Преобразование Фурье свертки обобщенных функций. Пусть прямое произведение  обобщенных функций f и gиз
обобщенных функций f и gиз  допускает расширение на функции вида
допускает расширение на функции вида 
 Именно, пусть для любой последовательности
Именно, пусть для любой последовательности
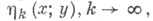 из
из  со свойствами:
со свойствами:

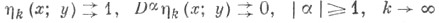 (равномерно на любом компакте), числовая последовательность
(равномерно на любом компакте), числовая последовательность 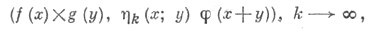 имеет предел, обозначаемый
имеет предел, обозначаемый  не зависящий от последовательности
не зависящий от последовательности  из указанного класса. В этом случае функционал f*g, действующий по формуле
из указанного класса. В этом случае функционал f*g, действующий по формуле
 наз. сверткой обобщенных функций f и g,
наз. сверткой обобщенных функций f и g,
 Свертка существует не для любых пар обобщенных функций f и g. Она заведомо существует, если при любом R> 0 множество
Свертка существует не для любых пар обобщенных функций f и g. Она заведомо существует, если при любом R> 0 множество 
ограничено в  (в частности, если f или gфинитна). Если свертка f * g существует, то она коммутативна, f * g = g* f, и коммутирует со сдвигом и с производной:
(в частности, если f или gфинитна). Если свертка f * g существует, то она коммутативна, f * g = g* f, и коммутирует со сдвигом и с производной: 
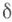 -функция Дирака играет роль лединицы
-функция Дирака играет роль лединицы


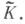 Тогда операция преобразования Фурье
Тогда операция преобразования Фурье  определяемая на пространстве обобщенных функций
определяемая на пространстве обобщенных функций  равенством
равенством  осуществляет изоморфизм
осуществляет изоморфизм  на пространство основных функций К'.
на пространство основных функций К'.  Здесь обратной операцией к Fслужит операция
Здесь обратной операцией к Fслужит операция 
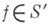
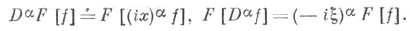
 где
где  -совокупность функций
-совокупность функций  таких, что
таких, что 
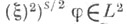 и
и 
 где Z - совокупность целых функций
где Z - совокупность целых функций  удовлетворяющих условию роста; существует число
удовлетворяющих условию роста; существует число 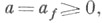 что для любого
что для любого 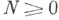 найдется С N > 0 такое, что
найдется С N > 0 такое, что 
 и ее можно разложить в тригонометрич. ряд
и ее можно разложить в тригонометрич. ряд 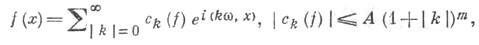
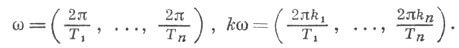
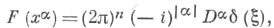 в частности
в частности 
 в частности
в частности 
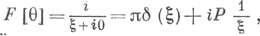 где
где  -функция Хeвисайда.
-функция Хeвисайда.  обобщенных функций f и gиз
обобщенных функций f и gиз  допускает расширение на функции вида
допускает расширение на функции вида 
 Именно, пусть для любой последовательности
Именно, пусть для любой последовательности 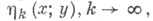 из
из  со свойствами:
со свойствами:

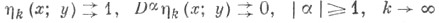 (равномерно на любом компакте), числовая последовательность
(равномерно на любом компакте), числовая последовательность 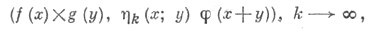 имеет предел, обозначаемый
имеет предел, обозначаемый  не зависящий от последовательности
не зависящий от последовательности  из указанного класса. В этом случае функционал f*g, действующий по формуле
из указанного класса. В этом случае функционал f*g, действующий по формуле  наз. сверткой обобщенных функций f и g,
наз. сверткой обобщенных функций f и g,
 Свертка существует не для любых пар обобщенных функций f и g. Она заведомо существует, если при любом R> 0 множество
Свертка существует не для любых пар обобщенных функций f и g. Она заведомо существует, если при любом R> 0 множество 
 (в частности, если f или gфинитна). Если свертка f * g существует, то она коммутативна, f * g = g* f, и коммутирует со сдвигом и с производной:
(в частности, если f или gфинитна). Если свертка f * g существует, то она коммутативна, f * g = g* f, и коммутирует со сдвигом и с производной: 
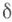 -функция Дирака играет роль лединицы
-функция Дирака играет роль лединицы