"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ ИНТЕГРАЛЬНЫЙ ОПЕРАТОР
Значение ФУРЬЕ ИНТЕГРАЛЬНЫЙ ОПЕРАТОР в математической энциклопедии:
интегральный оператор, обобщенное ядро к-рого является быстроосциллирующей функцией или интегралом от такой функции. Операторы такого типа возникли при исследовании асимптотики быстроосциллирующих решений уравнений с частными производными (см. [1], [2]) и при исследовании особенностей фундаментальных решений гиперболич. уравнений (см. [1], [2], [3]).
I. Канонический оператор Маслова (КОМ). Пусть  есть n-мерное лагранжево многообразие класса
есть n-мерное лагранжево многообразие класса  в фазовом пространстве
в фазовом пространстве  где х
где х 
 и
и  -объем на А. Каноническим атласом наз. локально конечное счетное покрытие многообразия
-объем на А. Каноническим атласом наз. локально конечное счетное покрытие многообразия  ограниченными односвязными областями
ограниченными односвязными областями  (картами), в каждой из к-рых в качестве координат можно взять либо переменные х, либо р, либо смешанный набор
(картами), в каждой из к-рых в качестве координат можно взять либо переменные х, либо р, либо смешанный набор

не содержащий сопряженных пар (pj, х j). КОМ действует из  в
в 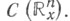 Канонич. операторы вводятся следующим образом.
Канонич. операторы вводятся следующим образом. 
1) Пусть карта  -неособая, т. е.
-неособая, т. е.  задается уравнением р = р (х)и
задается уравнением р = р (х)и

Здесь  -параметр,
-параметр,  -фиксированная точка,
-фиксированная точка,  и функция
и функция 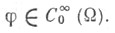
2) Пусть в карте  локальные координаты суть р, т. е.
локальные координаты суть р, т. е. задается уравнением х = х (р)и пусть
задается уравнением х = х (р)и пусть

Здесь F-1 есть  -преобразование Фурье
-преобразование Фурье

Аналогично определяется  в случае, когда координаты в
в случае, когда координаты в  -набор
-набор  Пусть
Пусть  и индекс Маслова
и индекс Маслова  для любого замкнутого пути l, лежащего на
для любого замкнутого пути l, лежащего на  Вводится разбиение единицы класса
Вводится разбиение единицы класса 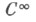 на
на 
 при
при 
и фиксируется точка  КОМ определяется формулой
КОМ определяется формулой

и  -индекс Маслова цепочки карт, соединяющих карты
-индекс Маслова цепочки карт, соединяющих карты  и
и 
Точка  наз. неособой, если в ее окрестности
наз. неособой, если в ее окрестности  задается уравнением р=р (х). Пусть пересечение карт
задается уравнением р=р (х). Пусть пересечение карт  непусто и связно,
непусто и связно,  -неособая точка и
-неособая точка и  -координаты в этих картах. Индексом Маслова пары карт
-координаты в этих картах. Индексом Маслова пары карт  наз. число
наз. число

где  -число отрицательных собственных значений матрицы А. Индекс Маслова цепочки карт определяется по аддитивности. Аналогично определяется индекс Маслова ind l пути l. Индекс Маслова ind (mod 4) пути на лагранжевом многообразии есть целочисленный гомотопич. инвариант (см. [1], [3]). КОМ инвариантен относительно выбора канонич. атласа локальных координат в картах и разбиения единицы, в следующем смысле: если
-число отрицательных собственных значений матрицы А. Индекс Маслова цепочки карт определяется по аддитивности. Аналогично определяется индекс Маслова ind l пути l. Индекс Маслова ind (mod 4) пути на лагранжевом многообразии есть целочисленный гомотопич. инвариант (см. [1], [3]). КОМ инвариантен относительно выбора канонич. атласа локальных координат в картах и разбиения единицы, в следующем смысле: если  -два КОМ, то в
-два КОМ, то в 

для любой функции 
Важнейший результат теории КОМ - формула коммутации КОМ и  -дифференциального (или
-дифференциального (или  -псевдодифференциального [3]) оператора.
-псевдодифференциального [3]) оператора.
Пусть  - дифференциальный оператор с действительным символом L( х, р )класса
- дифференциальный оператор с действительным символом L( х, р )класса  и выполнены условия: L( х, р)=0 на
и выполнены условия: L( х, р)=0 на  Многообразие
Многообразие  и объем
и объем  инвариантны относительно гамильтоновой системы
инвариантны относительно гамильтоновой системы

Тогда справедлива формула коммутации (здесь 

где  -производная в силу гамильтоновой системы. Следующие члены разложения (1) и оценки остаточных членов см. [3]. Уравнение
-производная в силу гамильтоновой системы. Следующие члены разложения (1) и оценки остаточных членов см. [3]. Уравнение  наз. уравнением переноса. Из формулы коммутации следует, что если
наз. уравнением переноса. Из формулы коммутации следует, что если  то функция
то функция  есть формальное асимптотич. решение уравнения
есть формальное асимптотич. решение уравнения 
Метод КОМ позволил решить следующие задачи.
1) Построение асимптотики решения задачи Коши с быстроосциллирующими начальными данными в большом (т. е. за любое конечное время) для строго гиперболич. систем дифференциальных уравнений с частными производными, для систем Дирака, Максвелла, теории упругости, для уравнения Шрёдингера (см. [1], [9] - [6], а также Квазиклассические приближение), а также решения нек-рых смешанных задач [4].
2) Построение асимптотики серий собственных значений самосопряженных дифференциальных операторов, ассоциированных с инвариантными относительно соответствующей гамильтоновой системы лагранжевыми многообразиями (см. [1], [3]).
3) Построение асимптотич. разложения по гладкости фундаментального решения строго гиперболич. системы уравнений с частными производными (см. [1], [5], [6]).
4) Построение коротковолновой асимптотики функции Грина, решения задачи о рассеянии и амплитуды рассеяния для уравнения Шрёдингера асимптотики спектральной функции (см. [5] - [7]).
Развит новый вариант КОМ на лагранжевых многообразиях с комплексным ростком (см. [8], [9]).
II. Интегральный оператор Фурье (ИОФ).
Пусть X, Y - ограниченные области в  N=N1 + N2,
N=N1 + N2, и
и  ИОФ наз. оператор
ИОФ наз. оператор

Здесь  (фазовая функция) - действительная и положительно однородная по
(фазовая функция) - действительная и положительно однородная по  порядка 1,
порядка 1,  и
и  при
при  Функция
Функция  (символ) и в простейшем случае разлагается при
(символ) и в простейшем случае разлагается при  в асимптотич. ряд
в асимптотич. ряд

Интеграл (2) сходится после соответствующей регуляризации и определяет непрерывный линейный оператор  Ядро оператора Аравно
Ядро оператора Аравно

Функция  и бесконечно дифференцируема вне проекции
и бесконечно дифференцируема вне проекции  на
на  множества
множества 
 Особенности Кзависят только от тейлоровского разложения символа рвокрестности С(при фиксированной фазе
Особенности Кзависят только от тейлоровского разложения символа рвокрестности С(при фиксированной фазе  Пусть фаза
Пусть фаза  невырождена, т. е. дифференциалы
невырождена, т. е. дифференциалы 
 линейно независимы на С';тогда С - гладкое многообразие размерности п. Оператору Аотвечает гладкое, коническое (по переменному
линейно независимы на С';тогда С - гладкое многообразие размерности п. Оператору Аотвечает гладкое, коническое (по переменному  двойственному к z =(x, у ))лагранжево многообразие
двойственному к z =(x, у ))лагранжево многообразие  размерности n-образ Спри отображении
размерности n-образ Спри отображении

В дальнейшем оператор Арассматривается на плотностях и(у)порядка 1/2:
 т. е.
т. е. 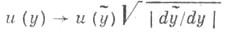 при замене переменных
при замене переменных  Символу рставится в соответствие плотность
Символу рставится в соответствие плотность  порядка 1/2 на
порядка 1/2 на  к-рая является образом
к-рая является образом  при отображении (3), где
при отображении (3), где  и
и 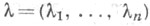 - координаты на
- координаты на  первого порядка однородности по
первого порядка однородности по  перенесенные с помощью (3) на С. Плотность bпри
перенесенные с помощью (3) на С. Плотность bпри  разлагается в асимптотич. ряд
разлагается в асимптотич. ряд

коэффициент b0 наз. главным символом оператора А. Пусть оператор Апредставим в виде (2), но с другой невырожденной фазовой функцией  и с другим символом
и с другим символом  Тогда для этого представления многообразие
Тогда для этого представления многообразие  остается прежним, величина
остается прежним, величина  постоянна, а главный символ
постоянна, а главный символ  равен
равен 
Общее определение ИОФ таково. Пусть X, Y- гладкие многообразия размерности N1, N2 и 
 -конич. гладкое лагранжево многообразие размерности п = N1+N2. Для любой точки
-конич. гладкое лагранжево многообразие размерности п = N1+N2. Для любой точки  существует невырожденная фазовая функция такая, что построенное по ней лагранжево многообразие локально совпадает с
существует невырожденная фазовая функция такая, что построенное по ней лагранжево многообразие локально совпадает с 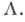 Пусть
Пусть 
 - множество объектов, состоящих из:
- множество объектов, состоящих из:
а) локальных координатных окрестностей 
 с локальными координатами
с локальными координатами  z =(x, у);
z =(x, у);
б) целого числа N и невырожденной фазовой функции  определенной в
определенной в  и такой, что отображение
и такой, что отображение

есть диффеоморфизм на открытое подмножество 
ИОФ наз. оператор  где А j имеет вид (2), N = Nj,
где А j имеет вид (2), N = Nj,  и носитель символа р= pj содержится в множестве
и носитель символа р= pj содержится в множестве 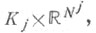 К j - компакт в
К j - компакт в  Класс таких операторов Aобозначают I т(L).
Класс таких операторов Aобозначают I т(L).
Пусть  -множество однородных порядка
-множество однородных порядка  по
по  плотностей на
плотностей на  порядка 1/2. По главным символам
порядка 1/2. По главным символам  операторов AJ естественным образом строится главный символ
операторов AJ естественным образом строится главный символ 
 оператора А, так что отображение
оператора А, так что отображение

есть изоморфизм (см. [2], [14]).
Наиболее важным для приложений ИОФ к дифференциальным уравнениям с частными производными является случай, когда проекции  - локальные диффеоморфизмы. Тогда N1=N2. и плотность d С -равна
- локальные диффеоморфизмы. Тогда N1=N2. и плотность d С -равна

и ограничен оператор

Так же, как и для КОМ, для ИОФ есть формулы коммутации с дифференциальными операторами со всеми вытекающими из них следствиями. Локально ИОФ можно представить в виде интеграла по параметру от КОМ (см. [10]). ИОФ применяется:
1) Для построения параметрикса и изучения микролокальной структуры особенностей (волновых фронтов) решений, гиперболич. уравнений, уравнений главного типа и краевых задач (см. [2], [14]).
2) При исследовании вопроса о локальной и глобальной разрешимости и субэллиптичности уравнений (см. [12]).
3) Для получения асимптотики спектральной функции псевдодифференциальных операторов (см. [13]).
Лит.:[1] Маслов В. II., Теория возмущений и асимптотические методы, М., 1965; [2] Xёрмандер Л., лМатематика

 есть n-мерное лагранжево многообразие класса
есть n-мерное лагранжево многообразие класса  в фазовом пространстве
в фазовом пространстве  где х
где х 
 и
и  -объем на А. Каноническим атласом наз. локально конечное счетное покрытие многообразия
-объем на А. Каноническим атласом наз. локально конечное счетное покрытие многообразия  ограниченными односвязными областями
ограниченными односвязными областями  (картами), в каждой из к-рых в качестве координат можно взять либо переменные х, либо р, либо смешанный набор
(картами), в каждой из к-рых в качестве координат можно взять либо переменные х, либо р, либо смешанный набор 
 в
в 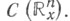 Канонич. операторы вводятся следующим образом.
Канонич. операторы вводятся следующим образом. 
 -неособая, т. е.
-неособая, т. е.  задается уравнением р = р (х)и
задается уравнением р = р (х)и 
 -параметр,
-параметр,  -фиксированная точка,
-фиксированная точка,  и функция
и функция 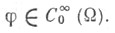
 локальные координаты суть р, т. е.
локальные координаты суть р, т. е. задается уравнением х = х (р)и пусть
задается уравнением х = х (р)и пусть 
 -преобразование Фурье
-преобразование Фурье 
 в случае, когда координаты в
в случае, когда координаты в  -набор
-набор  Пусть
Пусть  и индекс Маслова
и индекс Маслова  для любого замкнутого пути l, лежащего на
для любого замкнутого пути l, лежащего на  Вводится разбиение единицы класса
Вводится разбиение единицы класса 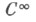 на
на 
 при
при 
 КОМ определяется формулой
КОМ определяется формулой 
 -индекс Маслова цепочки карт, соединяющих карты
-индекс Маслова цепочки карт, соединяющих карты  и
и 
 наз. неособой, если в ее окрестности
наз. неособой, если в ее окрестности  задается уравнением р=р (х). Пусть пересечение карт
задается уравнением р=р (х). Пусть пересечение карт  непусто и связно,
непусто и связно,  -неособая точка и
-неособая точка и  -координаты в этих картах. Индексом Маслова пары карт
-координаты в этих картах. Индексом Маслова пары карт  наз. число
наз. число 
 -число отрицательных собственных значений матрицы А. Индекс Маслова цепочки карт определяется по аддитивности. Аналогично определяется индекс Маслова ind l пути l. Индекс Маслова ind (mod 4) пути на лагранжевом многообразии есть целочисленный гомотопич. инвариант (см. [1], [3]). КОМ инвариантен относительно выбора канонич. атласа локальных координат в картах и разбиения единицы, в следующем смысле: если
-число отрицательных собственных значений матрицы А. Индекс Маслова цепочки карт определяется по аддитивности. Аналогично определяется индекс Маслова ind l пути l. Индекс Маслова ind (mod 4) пути на лагранжевом многообразии есть целочисленный гомотопич. инвариант (см. [1], [3]). КОМ инвариантен относительно выбора канонич. атласа локальных координат в картах и разбиения единицы, в следующем смысле: если  -два КОМ, то в
-два КОМ, то в 


 -дифференциального (или
-дифференциального (или  -псевдодифференциального [3]) оператора.
-псевдодифференциального [3]) оператора.  - дифференциальный оператор с действительным символом L( х, р )класса
- дифференциальный оператор с действительным символом L( х, р )класса  и выполнены условия: L( х, р)=0 на
и выполнены условия: L( х, р)=0 на  Многообразие
Многообразие  и объем
и объем  инвариантны относительно гамильтоновой системы
инвариантны относительно гамильтоновой системы 


 -производная в силу гамильтоновой системы. Следующие члены разложения (1) и оценки остаточных членов см. [3]. Уравнение
-производная в силу гамильтоновой системы. Следующие члены разложения (1) и оценки остаточных членов см. [3]. Уравнение  наз. уравнением переноса. Из формулы коммутации следует, что если
наз. уравнением переноса. Из формулы коммутации следует, что если  то функция
то функция  есть формальное асимптотич. решение уравнения
есть формальное асимптотич. решение уравнения 
 N=N1 + N2,
N=N1 + N2, и
и  ИОФ наз. оператор
ИОФ наз. оператор 
 (фазовая функция) - действительная и положительно однородная по
(фазовая функция) - действительная и положительно однородная по  порядка 1,
порядка 1,  и
и  при
при  Функция
Функция  (символ) и в простейшем случае разлагается при
(символ) и в простейшем случае разлагается при  в асимптотич. ряд
в асимптотич. ряд 
 Ядро оператора Аравно
Ядро оператора Аравно 
 и бесконечно дифференцируема вне проекции
и бесконечно дифференцируема вне проекции  на
на  множества
множества 
 Особенности Кзависят только от тейлоровского разложения символа рвокрестности С(при фиксированной фазе
Особенности Кзависят только от тейлоровского разложения символа рвокрестности С(при фиксированной фазе  Пусть фаза
Пусть фаза  невырождена, т. е. дифференциалы
невырождена, т. е. дифференциалы 
 линейно независимы на С';тогда С - гладкое многообразие размерности п. Оператору Аотвечает гладкое, коническое (по переменному
линейно независимы на С';тогда С - гладкое многообразие размерности п. Оператору Аотвечает гладкое, коническое (по переменному  двойственному к z =(x, у ))лагранжево многообразие
двойственному к z =(x, у ))лагранжево многообразие  размерности n-образ Спри отображении
размерности n-образ Спри отображении 
 т. е.
т. е. 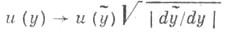 при замене переменных
при замене переменных  Символу рставится в соответствие плотность
Символу рставится в соответствие плотность  порядка 1/2 на
порядка 1/2 на  к-рая является образом
к-рая является образом  при отображении (3), где
при отображении (3), где  и
и 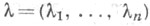 - координаты на
- координаты на  первого порядка однородности по
первого порядка однородности по  перенесенные с помощью (3) на С. Плотность bпри
перенесенные с помощью (3) на С. Плотность bпри  разлагается в асимптотич. ряд
разлагается в асимптотич. ряд 
 и с другим символом
и с другим символом  Тогда для этого представления многообразие
Тогда для этого представления многообразие  остается прежним, величина
остается прежним, величина  постоянна, а главный символ
постоянна, а главный символ  равен
равен 

 -конич. гладкое лагранжево многообразие размерности п = N1+N2. Для любой точки
-конич. гладкое лагранжево многообразие размерности п = N1+N2. Для любой точки  существует невырожденная фазовая функция такая, что построенное по ней лагранжево многообразие локально совпадает с
существует невырожденная фазовая функция такая, что построенное по ней лагранжево многообразие локально совпадает с 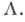 Пусть
Пусть 
 - множество объектов, состоящих из:
- множество объектов, состоящих из: 
 с локальными координатами
с локальными координатами  z =(x, у);
z =(x, у);  определенной в
определенной в  и такой, что отображение
и такой, что отображение 

 где А j имеет вид (2), N = Nj,
где А j имеет вид (2), N = Nj,  и носитель символа р= pj содержится в множестве
и носитель символа р= pj содержится в множестве 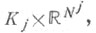 К j - компакт в
К j - компакт в  Класс таких операторов Aобозначают I т(L).
Класс таких операторов Aобозначают I т(L).  -множество однородных порядка
-множество однородных порядка  по
по  плотностей на
плотностей на  порядка 1/2. По главным символам
порядка 1/2. По главным символам  операторов AJ естественным образом строится главный символ
операторов AJ естественным образом строится главный символ 
 оператора А, так что отображение
оператора А, так что отображение 
 - локальные диффеоморфизмы. Тогда N1=N2. и плотность d С -равна
- локальные диффеоморфизмы. Тогда N1=N2. и плотность d С -равна 
