"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУНКЦИОНАЛЗначение ФУНКЦИОНАЛ в математической энциклопедии:
от марковского процесса - случайная величина или случайная функция, зависящая измеримым образом от траектории марковского процесса; условие измеримости варьируется в зависимости от конкретной ситуации. В общей теории марковских процессов принимается следующее определение Ф. Пусть в измеримом пространстве  задан необрывающийся однородный марковский процесс задан необрывающийся однородный марковский процесс  с операторами временного сдвига с операторами временного сдвига  и пусть и пусть  -наименьшая из -наименьшая из  -алгебр в пространстве элементарных событий, содержащих любое событие вида -алгебр в пространстве элементарных событий, содержащих любое событие вида  где где 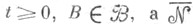 - пересечение всех пополнений - пересечение всех пополнений  по всевозможным мерам по всевозможным мерам  Случайная функция Случайная функция 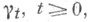 наз. функционалом от марковского процесса Х, если при каждом наз. функционалом от марковского процесса Х, если при каждом  величина величина  измерима относительно измерима относительно  -алгебры -алгебры 
Особый интерес представляют мультипликативные и аддитивные Ф. от марковских процессов. Первые из них выделяются условием  вторые - условием вторые - условием  причем функцию причем функцию  считают непрерывной справа на считают непрерывной справа на  (с другой стороны, иногда приходится предполагать эти условия выполняющимися лишь Р х -почти наверное для любых фиксированных (с другой стороны, иногда приходится предполагать эти условия выполняющимися лишь Р х -почти наверное для любых фиксированных  Соответствующие формулировки принимаются в случае обрывающихся и неоднородных процессов. Примеры аддитивных Ф. от марковского процесса Соответствующие формулировки принимаются в случае обрывающихся и неоднородных процессов. Примеры аддитивных Ф. от марковского процесса  можно получить, приравняв можно получить, приравняв 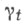 при при  или к или к  или к сумме скачков случайной функции f(xs )при или к сумме скачков случайной функции f(xs )при  где f(х) - ограниченная и измеримая относительно где f(х) - ограниченная и измеримая относительно 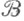 функция (второй и третий примеры корректны лишь при нек-рых дополнительных условиях). Переход от любого аддитивного Ф. функция (второй и третий примеры корректны лишь при нек-рых дополнительных условиях). Переход от любого аддитивного Ф. 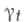 к ехр к ехр  доставляет пример мультипликативного Ф. В случае стандартного марковского процесса интересным и важным примером мультипликативного Ф. служит случайная функция, равная 1 при доставляет пример мультипликативного Ф. В случае стандартного марковского процесса интересным и важным примером мультипликативного Ф. служит случайная функция, равная 1 при  и 0 при и 0 при  где где 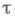 -момент первого выхода Xиз нек-рого множества -момент первого выхода Xиз нек-рого множества  
С мультипликативными Ф., подчиненными условию  связано одно естественное преобразование марковского процесса -переход к подпроцессу. По переходной функции Р(t, х, В )процесса связано одно естественное преобразование марковского процесса -переход к подпроцессу. По переходной функции Р(t, х, В )процесса   строят новую строят новую 
причем может оказаться, что  в нек-рых точках в нек-рых точках  Новой переходной функции в Новой переходной функции в  соответствует нек-рый марковский процесс соответствует нек-рый марковский процесс   к-рый вместе с исходным можно реализовать на одном и том же пространстве элементарных событий с одними и теми же мерами к-рый вместе с исходным можно реализовать на одном и том же пространстве элементарных событий с одними и теми же мерами  причем так, что причем так, что 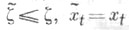 при при  и что и что  -алгебра -алгебра  является следом является следом  -алгебры -алгебры  в множестве в множестве  Процесс Процесс  наз. подпроцессом марковского процесса X, получаемым в результате лубивания наз. подпроцессом марковского процесса X, получаемым в результате лубивания
|

 задан необрывающийся однородный марковский процесс
задан необрывающийся однородный марковский процесс  с операторами временного сдвига
с операторами временного сдвига  и пусть
и пусть  -наименьшая из
-наименьшая из  -алгебр в пространстве элементарных событий, содержащих любое событие вида
-алгебр в пространстве элементарных событий, содержащих любое событие вида  где
где 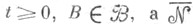 - пересечение всех пополнений
- пересечение всех пополнений  по всевозможным мерам
по всевозможным мерам  Случайная функция
Случайная функция 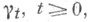 наз. функционалом от марковского процесса Х, если при каждом
наз. функционалом от марковского процесса Х, если при каждом  величина
величина  измерима относительно
измерима относительно  -алгебры
-алгебры 
 вторые - условием
вторые - условием  причем функцию
причем функцию  считают непрерывной справа на
считают непрерывной справа на  (с другой стороны, иногда приходится предполагать эти условия выполняющимися лишь Р х -почти наверное для любых фиксированных
(с другой стороны, иногда приходится предполагать эти условия выполняющимися лишь Р х -почти наверное для любых фиксированных  Соответствующие формулировки принимаются в случае обрывающихся и неоднородных процессов. Примеры аддитивных Ф. от марковского процесса
Соответствующие формулировки принимаются в случае обрывающихся и неоднородных процессов. Примеры аддитивных Ф. от марковского процесса  можно получить, приравняв
можно получить, приравняв 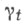 при
при  или к
или к  или к сумме скачков случайной функции f(xs )при
или к сумме скачков случайной функции f(xs )при  где f(х) - ограниченная и измеримая относительно
где f(х) - ограниченная и измеримая относительно 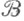 функция (второй и третий примеры корректны лишь при нек-рых дополнительных условиях). Переход от любого аддитивного Ф.
функция (второй и третий примеры корректны лишь при нек-рых дополнительных условиях). Переход от любого аддитивного Ф. 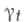 к ехр
к ехр  доставляет пример мультипликативного Ф. В случае стандартного марковского процесса интересным и важным примером мультипликативного Ф. служит случайная функция, равная 1 при
доставляет пример мультипликативного Ф. В случае стандартного марковского процесса интересным и важным примером мультипликативного Ф. служит случайная функция, равная 1 при  и 0 при
и 0 при  где
где 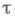 -момент первого выхода Xиз нек-рого множества
-момент первого выхода Xиз нек-рого множества 

 связано одно естественное преобразование марковского процесса -переход к подпроцессу. По переходной функции Р(t, х, В )процесса
связано одно естественное преобразование марковского процесса -переход к подпроцессу. По переходной функции Р(t, х, В )процесса 
 строят новую
строят новую 
 в нек-рых точках
в нек-рых точках  Новой переходной функции в
Новой переходной функции в  соответствует нек-рый марковский процесс
соответствует нек-рый марковский процесс 
 к-рый вместе с исходным можно реализовать на одном и том же пространстве элементарных событий с одними и теми же мерами
к-рый вместе с исходным можно реализовать на одном и том же пространстве элементарных событий с одними и теми же мерами  причем так, что
причем так, что 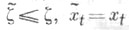 при
при  и что
и что  -алгебра
-алгебра  является следом
является следом  -алгебры
-алгебры  в множестве
в множестве  Процесс
Процесс  наз. подпроцессом марковского процесса X, получаемым в результате лубивания
наз. подпроцессом марковского процесса X, получаемым в результате лубивания