"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ
Значение ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ в математической энциклопедии:
линейной однородной системы обыкновенных дифференциальных уравнений - базис векторного пространства действительных (комплексных) решений этой системы. (Система может состоять и из одного уравнения.) Более подробно это определение формулируется следующим образом.
Множество действительных (комплексных) решений {x1(t),...,xn(t)}(заданных на нек-ром множестве Е)линейной однородной системы обыкновенных дифференциальных уравнений наз. Ф. с. р. этой системы уравнений (на множестве Е) при выполнении совокупности следующих двух условий: 1) если действительные (комплексные) числа С 1,..., С n таковы, что функция C1x1(t)+...+Cnxn(t) тождественно равна нулю на Е, то все числа С 1,..., С n равны нулю; 2) для всякого действительного (комплексного) решения х(t)рассматриваемой системы уравнений найдутся действительные (соответственно комплексные) числа С 1,..., С n (не зависящие от t)такие, что x(t) = C1x1(t)+...+Cnxn(t) при всех 
Если  -произвольная невырожденная
-произвольная невырожденная
 -матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то
-матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то  также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р.
также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р.
Если система дифференциальных уравнений имеет вид

где  (или
(или  а
а  (соответственно
(соответственно 
 причем отображение
причем отображение  суммируемо на каждом отрезке, содержащемся в
суммируемо на каждом отрезке, содержащемся в  - конечный или бесконечный интервал в
- конечный или бесконечный интервал в  то векторное пространство решений этой системы изоморфно
то векторное пространство решений этой системы изоморфно  (соответственно
(соответственно  Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений
Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений
 произвольная Ф. с. р. имеет вид
произвольная Ф. с. р. имеет вид

где  -произвольные линейно независимые векторы-столбцы.
-произвольные линейно независимые векторы-столбцы.
Всякая Ф. с. р. системы (1) имеет вид

где  - Коши оператор системы (1),
- Коши оператор системы (1),  - произвольное фиксированное число из интервала
- произвольное фиксированное число из интервала  а x1, . . ., х п - произвольный фиксированный базис пространства
а x1, . . ., х п - произвольный фиксированный базис пространства  (соответственно
(соответственно 
Если система дифференциальных уравнений состоит из одного уравнения

где функции
 суммируемы на каждом отрезке, содержащемся в
суммируемы на каждом отрезке, содержащемся в  (где
(где 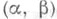 - конечный или бесконечный интервал в
- конечный или бесконечный интервал в  то векторное пространство решений этого уравнения изоморфно
то векторное пространство решений этого уравнения изоморфно  (соответственно
(соответственно  Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение
Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение  имеет Ф. с. р.
имеет Ф. с. р.  общее действительное решение этого уравнения дается формулой
общее действительное решение этого уравнения дается формулой  где C1, С2 - произвольные действительные постоянные.
где C1, С2 - произвольные действительные постоянные.
Если система дифференциальных уравнений имеет вид

где  (или
(или  ) и при всяком i = l, ..., k-1 отображение
) и при всяком i = l, ..., k-1 отображение

суммируемо на каждом отрезке, содержащемся в  (где
(где  -конечный или бесконечный интервал в
-конечный или бесконечный интервал в  то пространство решений этой системы уравнений изоморфно
то пространство решений этой системы уравнений изоморфно  (соответственно
(соответственно  Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.
Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.
Для линейных однородных систем дифференциальных уравнений, не разрешенных относительно старших производных, даже если коэффициенты системы постоянные, число решений, входящих в Ф. с. р. (т. е. размерность векторного пространства решений), вычисляется иногда не столь просто, как в вышеприведенных случаях. (В [1], з 11 рассмотрено такое вычисление для линейных систем дифференциальных уравнений с постоянными коэффициентами, не разрешенных относительно старших производных.)
Лит.:[1] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974.
В. М. Миллионщиков.


 -произвольная невырожденная
-произвольная невырожденная
 -матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то
-матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то  также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р.
также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р. 
 (или
(или  а
а  (соответственно
(соответственно 
 причем отображение
причем отображение  суммируемо на каждом отрезке, содержащемся в
суммируемо на каждом отрезке, содержащемся в  - конечный или бесконечный интервал в
- конечный или бесконечный интервал в  то векторное пространство решений этой системы изоморфно
то векторное пространство решений этой системы изоморфно  (соответственно
(соответственно  Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений
Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений  произвольная Ф. с. р. имеет вид
произвольная Ф. с. р. имеет вид 
 -произвольные линейно независимые векторы-столбцы.
-произвольные линейно независимые векторы-столбцы. 
 - Коши оператор системы (1),
- Коши оператор системы (1),  - произвольное фиксированное число из интервала
- произвольное фиксированное число из интервала  а x1, . . ., х п - произвольный фиксированный базис пространства
а x1, . . ., х п - произвольный фиксированный базис пространства  (соответственно
(соответственно 

 суммируемы на каждом отрезке, содержащемся в
суммируемы на каждом отрезке, содержащемся в  (где
(где 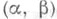 - конечный или бесконечный интервал в
- конечный или бесконечный интервал в  то векторное пространство решений этого уравнения изоморфно
то векторное пространство решений этого уравнения изоморфно  (соответственно
(соответственно  Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение
Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение  имеет Ф. с. р.
имеет Ф. с. р.  общее действительное решение этого уравнения дается формулой
общее действительное решение этого уравнения дается формулой  где C1, С2 - произвольные действительные постоянные.
где C1, С2 - произвольные действительные постоянные. 
 (или
(или  ) и при всяком i = l, ..., k-1 отображение
) и при всяком i = l, ..., k-1 отображение 
 (где
(где  -конечный или бесконечный интервал в
-конечный или бесконечный интервал в  то пространство решений этой системы уравнений изоморфно
то пространство решений этой системы уравнений изоморфно  (соответственно
(соответственно  Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.
Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.