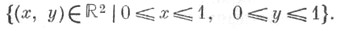"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУНДАМЕНТАЛЬНАЯ ОБЛАСТЬЗначение ФУНДАМЕНТАЛЬНАЯ ОБЛАСТЬ в математической энциклопедии:
дискретной группы Г преобразований топологич. пространства X - подмножество 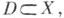 содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество 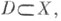 являющееся замыканием открытого подмножества и такое, что подмножества являющееся замыканием открытого подмножества и такое, что подмножества 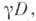 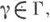 не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости 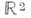 на целочисленные векторы может быть взят квадрат на целочисленные векторы может быть взят квадрат 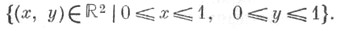
Выбор Ф. о., как правило, неоднозначен.
Э. Б. Винберг.
|

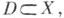 содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество
содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество 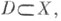 являющееся замыканием открытого подмножества и такое, что подмножества
являющееся замыканием открытого подмножества и такое, что подмножества 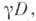
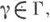 не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости
не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости 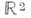 на целочисленные векторы может быть взят квадрат
на целочисленные векторы может быть взят квадрат