"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУНДАМЕНТАЛЬНАЯ ГРУППА
Значение ФУНДАМЕНТАЛЬНАЯ ГРУППА в математической энциклопедии:
группа Пуанкаре,- первая абсолютная гомотопическая группа  Пусть / - отрезок [0, 1],
Пусть / - отрезок [0, 1],  - его граница. Элементами Ф. г. пунктированного топологич. пространства (X, х0 )служат гомотопич. классы замкнутых путей в X, т. е. классы гомотопных rel {0, 1} непрерывных отображений пары
- его граница. Элементами Ф. г. пунктированного топологич. пространства (X, х0 )служат гомотопич. классы замкнутых путей в X, т. е. классы гомотопных rel {0, 1} непрерывных отображений пары 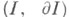 в (X, x0). Путь s1s2
в (X, x0). Путь s1s2

наз. произведением путей s1 и s2. Гомотопич. класс произведения зависит только от классов сомножителей, возникающая операция, вообще говоря, некоммутативна. Единицей служит класс постоянного отображения в x0, обратным к классу  содержащему путь
содержащему путь  служит класс пути
служит класс пути  Непрерывному отображению
Непрерывному отображению  соответствует гомоморфизм
соответствует гомоморфизм

т. е.  является функтором на категории топологич. пространств в категорию (неабелевых) групп. Для любого пути
является функтором на категории топологич. пространств в категорию (неабелевых) групп. Для любого пути 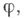 соединяющего точки x1 и х 2. определен изоморфизм
соединяющего точки x1 и х 2. определен изоморфизм

зависящий только от гомотопич. класса пути  Группа
Группа  действует автоморфизмами на
действует автоморфизмами на  в случае п -1 элемент
в случае п -1 элемент 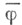 действует как внутренний автоморфизм
действует как внутренний автоморфизм  Гомоморфизм Гуревича
Гомоморфизм Гуревича  является эпиморфизмом с ядром
является эпиморфизмом с ядром 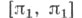 (теорема Пуанкаре).
(теорема Пуанкаре).
Линейно связное топологич. пространство с нулевой Ф. г. наз. односвязным. Ф. г. произведения  пространств изоморфна прямому произведению Ф. г. сомножителей:
пространств изоморфна прямому произведению Ф. г. сомножителей:  Пусть ( Х, х 0 )-линейно связное топологич. пространство,
Пусть ( Х, х 0 )-линейно связное топологич. пространство, 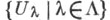 - покрытие Xзамкнутой относительно пересечений системой открытых множеств
- покрытие Xзамкнутой относительно пересечений системой открытых множеств  таких, что
таких, что  тогда
тогда  -прямой предел диаграммы
-прямой предел диаграммы  где
где 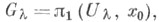 а
а  индуцировано включением
индуцировано включением  (теорема Зейферта - Ван Кампена). Напр., если дано покрытие, состоящее из U0, U1, U2. и
(теорема Зейферта - Ван Кампена). Напр., если дано покрытие, состоящее из U0, U1, U2. и  односвязно, то
односвязно, то 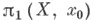 есть свободное произведение групп
есть свободное произведение групп  и
и 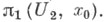 В случае клеточного пространства утверждение теоремы справедливо также для замкнутых клеточных подпространств в X.
В случае клеточного пространства утверждение теоремы справедливо также для замкнутых клеточных подпространств в X.
Для клеточного пространства X, нульмерный остов к-рого состоит из единственной точки х 0,каждая одномерная клетка  задает образующую Ф. г.
задает образующую Ф. г.  каждая двумерная клетка
каждая двумерная клетка  задает соотношение, отвечающее приклеивающему отображению клетки
задает соотношение, отвечающее приклеивающему отображению клетки 
Пусть Xобладает покрытием  таким, что гомоморфизм включения
таким, что гомоморфизм включения  нулевой для любой точки z. Тогда существует накрытие
нулевой для любой точки z. Тогда существует накрытие  с
с  В этом случае группа коммутирующих с ргомеоморфизмов пространства
В этом случае группа коммутирующих с ргомеоморфизмов пространства  на себя (скольжений) изоморфна
на себя (скольжений) изоморфна  порядок группы
порядок группы 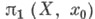 равен мощности слоя р -1 х 0. Для отображения
равен мощности слоя р -1 х 0. Для отображения 
 линейно связных пространств такого, что
линейно связных пространств такого, что 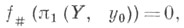 существует поднятие
существует поднятие 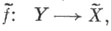
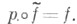 Накрытие
Накрытие  наз. универсальным.
наз. универсальным.
Лит.:[1] Масси У., Столлингс Дж., Алгебраическая топология, пер. о англ., М., 1977; [2] Рохлин В. А., Фукс Д. Б., Начальный курс топологии, М., 1977; [3] Спеньер 9., Алгебраическая топология, пер. с англ., М., 1971.
А. В. Хохлов.

 Пусть / - отрезок [0, 1],
Пусть / - отрезок [0, 1],  - его граница. Элементами Ф. г. пунктированного топологич. пространства (X, х0 )служат гомотопич. классы замкнутых путей в X, т. е. классы гомотопных rel {0, 1} непрерывных отображений пары
- его граница. Элементами Ф. г. пунктированного топологич. пространства (X, х0 )служат гомотопич. классы замкнутых путей в X, т. е. классы гомотопных rel {0, 1} непрерывных отображений пары 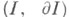 в (X, x0). Путь s1s2
в (X, x0). Путь s1s2 
 содержащему путь
содержащему путь  служит класс пути
служит класс пути  Непрерывному отображению
Непрерывному отображению  соответствует гомоморфизм
соответствует гомоморфизм 
 является функтором на категории топологич. пространств в категорию (неабелевых) групп. Для любого пути
является функтором на категории топологич. пространств в категорию (неабелевых) групп. Для любого пути 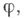 соединяющего точки x1 и х 2. определен изоморфизм
соединяющего точки x1 и х 2. определен изоморфизм 
 Группа
Группа  действует автоморфизмами на
действует автоморфизмами на  в случае п -1 элемент
в случае п -1 элемент 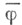 действует как внутренний автоморфизм
действует как внутренний автоморфизм  Гомоморфизм Гуревича
Гомоморфизм Гуревича  является эпиморфизмом с ядром
является эпиморфизмом с ядром 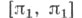 (теорема Пуанкаре).
(теорема Пуанкаре).  пространств изоморфна прямому произведению Ф. г. сомножителей:
пространств изоморфна прямому произведению Ф. г. сомножителей:  Пусть ( Х, х 0 )-линейно связное топологич. пространство,
Пусть ( Х, х 0 )-линейно связное топологич. пространство, 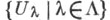 - покрытие Xзамкнутой относительно пересечений системой открытых множеств
- покрытие Xзамкнутой относительно пересечений системой открытых множеств  таких, что
таких, что  тогда
тогда  -прямой предел диаграммы
-прямой предел диаграммы  где
где 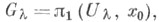 а
а  индуцировано включением
индуцировано включением  (теорема Зейферта - Ван Кампена). Напр., если дано покрытие, состоящее из U0, U1, U2. и
(теорема Зейферта - Ван Кампена). Напр., если дано покрытие, состоящее из U0, U1, U2. и  односвязно, то
односвязно, то 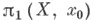 есть свободное произведение групп
есть свободное произведение групп  и
и 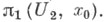 В случае клеточного пространства утверждение теоремы справедливо также для замкнутых клеточных подпространств в X.
В случае клеточного пространства утверждение теоремы справедливо также для замкнутых клеточных подпространств в X.  задает образующую Ф. г.
задает образующую Ф. г.  каждая двумерная клетка
каждая двумерная клетка  задает соотношение, отвечающее приклеивающему отображению клетки
задает соотношение, отвечающее приклеивающему отображению клетки 
 таким, что гомоморфизм включения
таким, что гомоморфизм включения  нулевой для любой точки z. Тогда существует накрытие
нулевой для любой точки z. Тогда существует накрытие  с
с  В этом случае группа коммутирующих с ргомеоморфизмов пространства
В этом случае группа коммутирующих с ргомеоморфизмов пространства  на себя (скольжений) изоморфна
на себя (скольжений) изоморфна  порядок группы
порядок группы 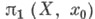 равен мощности слоя р -1 х 0. Для отображения
равен мощности слоя р -1 х 0. Для отображения 
 линейно связных пространств такого, что
линейно связных пространств такого, что 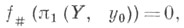 существует поднятие
существует поднятие 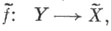
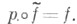 Накрытие
Накрытие  наз. универсальным.
наз. универсальным.