"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУКСА УРАВНЕНИЕ
Значение ФУКСА УРАВНЕНИЕ в математической энциклопедии:
уравнение класса Фукса - линейное однородное обыкновенное дифференциальное уравнение в комплексной области

с аналитич. оэффициентами, все особые точки к-рого на Римана сфере являются регулярными особыми точками. Для того чтобы уравнение (1) принадлежало классу Фукса, необходимо и достаточно, чтобы его коэффициенты имели вид

где z1, ..., zk - различные точки, qj(z) - многочлен степени  Система w'=A(z)wиз пуравнений принадлежит классу Фукса, если она имеет вид
Система w'=A(z)wиз пуравнений принадлежит классу Фукса, если она имеет вид

где z1, ..., zk - различные точки,  - постоянные матрицы порядка
- постоянные матрицы порядка  Особыми для уравнения (1) и системы (2,) являются точки z1, ..., zk, оо (бесконечность). Для Ф. у. (1) справедливо тождество Фукса:
Особыми для уравнения (1) и системы (2,) являются точки z1, ..., zk, оо (бесконечность). Для Ф. у. (1) справедливо тождество Фукса:

где  -характеристич. показатели в точке zm, а
-характеристич. показатели в точке zm, а  -в точке
-в точке  Ф. у. (и системы) наз. также регулярными уравнениями (системами). Этот класс уравнений и систем был введен Л. Фуксом [1].
Ф. у. (и системы) наз. также регулярными уравнениями (системами). Этот класс уравнений и систем был введен Л. Фуксом [1].
Пусть D- сфера Римана с проколами в точках z1, ..., zk,  Любое нетривиальное решение Ф. у. (1) (соответственно любая компонента решения системы (2)) есть аналитическая в области Dфункция. Как правило, эта функция бесконечнозначна, а все особые точки уравнения (1) (системы (2)) являются ее точками ветвления бесконечного порядка.
Любое нетривиальное решение Ф. у. (1) (соответственно любая компонента решения системы (2)) есть аналитическая в области Dфункция. Как правило, эта функция бесконечнозначна, а все особые точки уравнения (1) (системы (2)) являются ее точками ветвления бесконечного порядка.
Ф. у. 2-го порядка с особыми точками  имеет вид
имеет вид

где Qk-2 (z) - многочлен степени k-2. Преобразование  переводит Ф. у. в Ф. у., причем
переводит Ф. у. в Ф. у., причем

а характеристич. показатели в остальных особых точках не меняются. С помощью таких преобразований уравнение (3) приводится к виду

Ф. у. 2-го порядка, имеющее Nособых точек, полностью определяется заданием характеристич. показателей в этих точках тогда и только тогда, когда N<4. С помощью дробно-линейного преобразования уравнение приводится к виду: a) N=1, б) N=2,
б) N=2, (Эйлера уравнение); в) N=3 - Папперица уравнение (или уравнение Римана).
(Эйлера уравнение); в) N=3 - Папперица уравнение (или уравнение Римана).
Матричное Ф. у. имеет вид
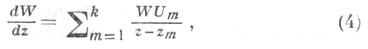
где z1, ..., zk - различные точки, W- матрица-функция порядка  -постоянные матрицы. Матрица U т наз. дифференциальной подстановкой в точке zm. Пусть
-постоянные матрицы. Матрица U т наз. дифференциальной подстановкой в точке zm. Пусть 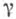 - простая замкнутая кривая с началом в неособой точке b, положительно ориентированная и содержащая внутри себя только одну особую точку zm. Если W(z)- голоморфное в точке bрешение уравнения (4), то при
- простая замкнутая кривая с началом в неособой точке b, положительно ориентированная и содержащая внутри себя только одну особую точку zm. Если W(z)- голоморфное в точке bрешение уравнения (4), то при  аналитич. родолжении вдоль
аналитич. родолжении вдоль  где V т - постоянная матрица, наз. интегральной подстановкой в z т. А. Пуанкаре (Н. Poincare, см. [2]) поставил для систем вида (4) задачу, к-рая наз. прямой регулярной задачей Пуанкаре. Она состоит из следующих трех задач:
где V т - постоянная матрица, наз. интегральной подстановкой в z т. А. Пуанкаре (Н. Poincare, см. [2]) поставил для систем вида (4) задачу, к-рая наз. прямой регулярной задачей Пуанкаре. Она состоит из следующих трех задач:
A) представление решения W(z)во всей области его существования;
Б) построение интегральных подстановок в точках 2m;
B) аналитич. характеристика особенностей решений.
В частности, решение задачи Б) позволяет построить группу монодромии уравнения (4). Решение задачи Пуанкаре было получено И. А. Лаппо-Данилевскйм [3]. Пусть 
- гиперлогарифмы:

W0(z) - элемент (росток) в точке Ь решения уравнения (4), нормированный условием W0(b)=I и W(z) - аналитическая в области . матрица-функция, порожденная этим элементом. Тогда W(z)есть целая функция от матриц U1 ,. . ., Uk и разлагается в ряд

к-рый сходится равномерно по z на любом компакте  Интегральная подстановка Vm в точке zm, отвечающая решению W(z), есть целая функция от матриц U1...., Uk и разлагается в ряд
Интегральная подстановка Vm в точке zm, отвечающая решению W(z), есть целая функция от матриц U1...., Uk и разлагается в ряд

где Pj выражаются через гиперлогарифмы (см. [3], [6]).
Получены также формулы, дающие решение задачи В) (см. [3]).
Лит.:[1] Fuchs L., лJ. reine und angew. Math.



 Система w'=A(z)wиз пуравнений принадлежит классу Фукса, если она имеет вид
Система w'=A(z)wиз пуравнений принадлежит классу Фукса, если она имеет вид 
 - постоянные матрицы порядка
- постоянные матрицы порядка  Особыми для уравнения (1) и системы (2,) являются точки z1, ..., zk, оо (бесконечность). Для Ф. у. (1) справедливо тождество Фукса:
Особыми для уравнения (1) и системы (2,) являются точки z1, ..., zk, оо (бесконечность). Для Ф. у. (1) справедливо тождество Фукса: 
 -характеристич. показатели в точке zm, а
-характеристич. показатели в точке zm, а  -в точке
-в точке  Ф. у. (и системы) наз. также регулярными уравнениями (системами). Этот класс уравнений и систем был введен Л. Фуксом [1].
Ф. у. (и системы) наз. также регулярными уравнениями (системами). Этот класс уравнений и систем был введен Л. Фуксом [1].  Любое нетривиальное решение Ф. у. (1) (соответственно любая компонента решения системы (2)) есть аналитическая в области Dфункция. Как правило, эта функция бесконечнозначна, а все особые точки уравнения (1) (системы (2)) являются ее точками ветвления бесконечного порядка.
Любое нетривиальное решение Ф. у. (1) (соответственно любая компонента решения системы (2)) есть аналитическая в области Dфункция. Как правило, эта функция бесконечнозначна, а все особые точки уравнения (1) (системы (2)) являются ее точками ветвления бесконечного порядка.  имеет вид
имеет вид 
 переводит Ф. у. в Ф. у., причем
переводит Ф. у. в Ф. у., причем 

 б) N=2,
б) N=2, (Эйлера уравнение); в) N=3 - Папперица уравнение (или уравнение Римана).
(Эйлера уравнение); в) N=3 - Папперица уравнение (или уравнение Римана). 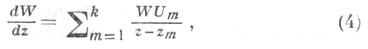
 -постоянные матрицы. Матрица U т наз. дифференциальной подстановкой в точке zm. Пусть
-постоянные матрицы. Матрица U т наз. дифференциальной подстановкой в точке zm. Пусть 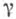 - простая замкнутая кривая с началом в неособой точке b, положительно ориентированная и содержащая внутри себя только одну особую точку zm. Если W(z)- голоморфное в точке bрешение уравнения (4), то при
- простая замкнутая кривая с началом в неособой точке b, положительно ориентированная и содержащая внутри себя только одну особую точку zm. Если W(z)- голоморфное в точке bрешение уравнения (4), то при  аналитич. родолжении вдоль
аналитич. родолжении вдоль  где V т - постоянная матрица, наз. интегральной подстановкой в z т. А. Пуанкаре (Н. Poincare, см. [2]) поставил для систем вида (4) задачу, к-рая наз. прямой регулярной задачей Пуанкаре. Она состоит из следующих трех задач:
где V т - постоянная матрица, наз. интегральной подстановкой в z т. А. Пуанкаре (Н. Poincare, см. [2]) поставил для систем вида (4) задачу, к-рая наз. прямой регулярной задачей Пуанкаре. Она состоит из следующих трех задач: 


 Интегральная подстановка Vm в точке zm, отвечающая решению W(z), есть целая функция от матриц U1...., Uk и разлагается в ряд
Интегральная подстановка Vm в точке zm, отвечающая решению W(z), есть целая функция от матриц U1...., Uk и разлагается в ряд 