"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУБИНИ ТЕОРЕМАЗначение ФУБИНИ ТЕОРЕМА в математической энциклопедии:
теорема, устанавливающая связь между кратным интегралом и повторным. Пусть  и и  -измеримые пространства с -измеримые пространства с  -конечными полными мерами -конечными полными мерами  и и  определенными соответственно на определенными соответственно на 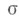 -алгебрах -алгебрах  и и  Если функция f( х, у )интегрируема на произведении Xx. пространств Xи Yпо произведению Если функция f( х, у )интегрируема на произведении Xx. пространств Xи Yпо произведению  мер мер  и и  то для почти всех то для почти всех  функция f( х, у )переменной хинтегрируема на пространстве . по мере функция f( х, у )переменной хинтегрируема на пространстве . по мере  функция функция  интегрируема на пространстве Yпо мере интегрируема на пространстве Yпо мере  и имеет место равенство и имеет место равенство  Ф. т. справедлива, в частности, для случая, когда Ф. т. справедлива, в частности, для случая, когда   и и  - меры Лебега соответственно в евклидовых пространствах - меры Лебега соответственно в евклидовых пространствах  (ти п- натуральные числа), (ти п- натуральные числа),
 f = f(x, y)-измеримая по Лебегу на пространстве f = f(x, y)-измеримая по Лебегу на пространстве  функция, функция,   При этих предположениях формула (1) имеет вид При этих предположениях формула (1) имеет вид

Для того чтобы в случае функции f, определенной на произвольном измеримом по Лебегу множестве  выразить кратный интеграл через повторный, нужно продолжить функцию f нулем на все пространство выразить кратный интеграл через повторный, нужно продолжить функцию f нулем на все пространство  и применить формулу (2). См. также Повторный интеграл. Ф. т. установлена Г. Фубини [1]. и применить формулу (2). См. также Повторный интеграл. Ф. т. установлена Г. Фубини [1]. Лит.:[1] Fubini G., Sugli integrali multipli (1907), Opere scelte, v. 2, Roma, 1958, p. 243 - 49.
Л. Д. Кудрявцев.
|

 и
и  -измеримые пространства с
-измеримые пространства с  -конечными полными мерами
-конечными полными мерами  и
и  определенными соответственно на
определенными соответственно на 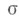 -алгебрах
-алгебрах  и
и  Если функция f( х, у )интегрируема на произведении Xx. пространств Xи Yпо произведению
Если функция f( х, у )интегрируема на произведении Xx. пространств Xи Yпо произведению  мер
мер  и
и  то для почти всех
то для почти всех  функция f( х, у )переменной хинтегрируема на пространстве . по мере
функция f( х, у )переменной хинтегрируема на пространстве . по мере  функция
функция  интегрируема на пространстве Yпо мере
интегрируема на пространстве Yпо мере  и имеет место равенство
и имеет место равенство  Ф. т. справедлива, в частности, для случая, когда
Ф. т. справедлива, в частности, для случая, когда 
 и
и  - меры Лебега соответственно в евклидовых пространствах
- меры Лебега соответственно в евклидовых пространствах  (ти п- натуральные числа),
(ти п- натуральные числа),  f = f(x, y)-измеримая по Лебегу на пространстве
f = f(x, y)-измеримая по Лебегу на пространстве  функция,
функция, 
 При этих предположениях формула (1) имеет вид
При этих предположениях формула (1) имеет вид 
 выразить кратный интеграл через повторный, нужно продолжить функцию f нулем на все пространство
выразить кратный интеграл через повторный, нужно продолжить функцию f нулем на все пространство  и применить формулу (2). См. также Повторный интеграл. Ф. т. установлена Г. Фубини [1].
и применить формулу (2). См. также Повторный интеграл. Ф. т. установлена Г. Фубини [1].