"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФРЕШЕ ДИФФЕРЕНЦИАЛ
Значение ФРЕШЕ ДИФФЕРЕНЦИАЛ в математической энциклопедии:
в точке x0 отображения  нормированною пространства Xв нормированное пространство Y- отображение
нормированною пространства Xв нормированное пространство Y- отображение  являющееся линейным и непрерывным отображением из Xв Yи обладающее тем свойством, что
являющееся линейным и непрерывным отображением из Xв Yи обладающее тем свойством, что

где

Если отображение f в точке x0 допускает разложение (1), то оно наз. дифференцируемым по Фреше, а сам оператор
 наз. Фреше производной.
наз. Фреше производной.
Для функции f конечного числа переменных Ф. д.- линейная функции
 обладающая тем свойством, что
обладающая тем свойством, что

где  или любая другая равносильная норма в
или любая другая равносильная норма в 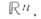 При этом
При этом 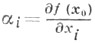 -частные производные функции f в точке x0.
-частные производные функции f в точке x0.
Определение (2), являющееся ныне общепринятым, впервые в явной форме появилось, по-видимому, в лекциях К. Вейерштрасса (1861, см. [1]). В кон. 19 в. это определение постепенно входит в учебники (см. [2], [3] и др.). Однако к моменту, когда М. Фреше (см. [4], [5]) начал разработку бесконечномерного анализа, классическое ныне определение дифференциала было настолько необщепринятым, что и сам М. Фреше полагал, что определенный им дифференциал на бесконечномерном пространстве является новым понятием и в конечномерном случае. В настоящее время термин употребляется лишь при рассмотрении бесконечномерных отображений. См. Гато дифференциал, Дифференцирование отображения.
Лит.:[1] Dugаc. P., Elements d'analyse de Karl Weierstrass. P., 1972; [2] Stоlz. О., Grundzuge der Differential-und Intesralrechnung, Bd 1, Lpz., 1893; [3] Young W., The fundamental theorems of the differential calculus, Camb., 1910; [4] Freсhet M., лC. r. Acad. sci.

 нормированною пространства Xв нормированное пространство Y- отображение
нормированною пространства Xв нормированное пространство Y- отображение  являющееся линейным и непрерывным отображением из Xв Yи обладающее тем свойством, что
являющееся линейным и непрерывным отображением из Xв Yи обладающее тем свойством, что 

 наз. Фреше производной.
наз. Фреше производной.  обладающая тем свойством, что
обладающая тем свойством, что 
 или любая другая равносильная норма в
или любая другая равносильная норма в 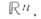 При этом
При этом 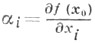 -частные производные функции f в точке x0.
-частные производные функции f в точке x0.