"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФРЕШЕ ВАРИАЦИЯЗначение ФРЕШЕ ВАРИАЦИЯ в математической энциклопедии:
- одна из числовых характеристик функции нескольких переменных, к-рую можно рассматривать как многомерный аналог вариации функции одного переменного. Пусть действительнозначная функция f(x)=f(xl, . . ., х n) задана на n-мерном параллелепипеде 
и введены обозначения

Пусть П - произвольное разбиение параллелепипеда Dn гиперплоскостями

на n-мерные параллелепипеды, а  могут принимать значения могут принимать значения  произвольным образом. Вариация Фреше определяется так: произвольным образом. Вариация Фреше определяется так: 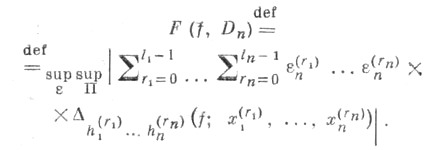
Если  то говорят, что функция f(х)имеет ограниченную (конечную) вариацию Фреше на Dn, а класс всех таких функций обозначается через F(Dn). Этот класс при п=2 введен М. Фреше [1] в связи с исследованием общего вида билинейного непрерывного функционала то говорят, что функция f(х)имеет ограниченную (конечную) вариацию Фреше на Dn, а класс всех таких функций обозначается через F(Dn). Этот класс при п=2 введен М. Фреше [1] в связи с исследованием общего вида билинейного непрерывного функционала  в пространстве непрерывных на квадрате в пространстве непрерывных на квадрате  функций вида функций вида  Он доказал, что всякий такой функционал представляется в виде Он доказал, что всякий такой функционал представляется в виде 
где

Для  -периодических функций класса F(Qn) -периодических функций класса F(Qn)  справедливы аналоги многих классических признаков сходимости рядов Фурье [2]. Например, если справедливы аналоги многих классических признаков сходимости рядов Фурье [2]. Например, если  то прямоугольные частичные суммы ряда Фурье функции f(x)в каждой точке х = (х 1, ..., х п )сходятся к числу то прямоугольные частичные суммы ряда Фурье функции f(x)в каждой точке х = (х 1, ..., х п )сходятся к числу
 где суммирование распространяется на. все 2т возможных комбинаций знаков где суммирование распространяется на. все 2т возможных комбинаций знаков  При этом, если функция непрерывна, то сходимость равномерная (аналог признака Жордана). При этом, если функция непрерывна, то сходимость равномерная (аналог признака Жордана).
Лит.:[1] Prechet M., лTrans. Аmеmr. Math. Soc.
|




 могут принимать значения
могут принимать значения  произвольным образом. Вариация Фреше определяется так:
произвольным образом. Вариация Фреше определяется так: 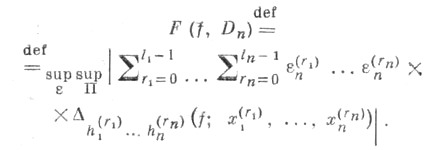
 то говорят, что функция f(х)имеет ограниченную (конечную) вариацию Фреше на Dn, а класс всех таких функций обозначается через F(Dn). Этот класс при п=2 введен М. Фреше [1] в связи с исследованием общего вида билинейного непрерывного функционала
то говорят, что функция f(х)имеет ограниченную (конечную) вариацию Фреше на Dn, а класс всех таких функций обозначается через F(Dn). Этот класс при п=2 введен М. Фреше [1] в связи с исследованием общего вида билинейного непрерывного функционала  в пространстве непрерывных на квадрате
в пространстве непрерывных на квадрате  функций вида
функций вида  Он доказал, что всякий такой функционал представляется в виде
Он доказал, что всякий такой функционал представляется в виде 

 -периодических функций класса F(Qn)
-периодических функций класса F(Qn)  справедливы аналоги многих классических признаков сходимости рядов Фурье [2]. Например, если
справедливы аналоги многих классических признаков сходимости рядов Фурье [2]. Например, если  то прямоугольные частичные суммы ряда Фурье функции f(x)в каждой точке х = (х 1, ..., х п )сходятся к числу
то прямоугольные частичные суммы ряда Фурье функции f(x)в каждой точке х = (х 1, ..., х п )сходятся к числу  где суммирование распространяется на. все 2т возможных комбинаций знаков
где суммирование распространяется на. все 2т возможных комбинаций знаков  При этом, если функция непрерывна, то сходимость равномерная (аналог признака Жордана).
При этом, если функция непрерывна, то сходимость равномерная (аналог признака Жордана).