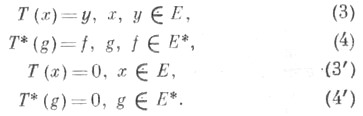"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФРЕДГОЛЬМА АЛЬТЕРНАТИВА
Значение ФРЕДГОЛЬМА АЛЬТЕРНАТИВА в математической энциклопедии:
- альтернативное утверждение, вытекающее из Фредгольма теорем. В случае линейного интегрального уравнения Фредгольма 2-го рода
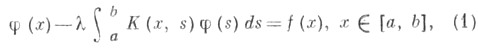
Ф. а. утверждает: либо уравнение (1) и сопряженное с ним уравнение

имеют единственные решения  каковы бы ни были известные функции f g, либо соответствующие однородные уравнения
каковы бы ни были известные функции f g, либо соответствующие однородные уравнения

имеют ненулевые решения, причем число линейно независимых решений конечно и одинаково для обоих уравнений.
Во втором случае для того чтобы уравнение (1) имело решение, необходимо и достатoчно, чтобы

где  -полная система линейно независимых решений уравнения (2'). При этом общее решение уравнения (1) имеет вид
-полная система линейно независимых решений уравнения (2'). При этом общее решение уравнения (1) имеет вид

где j k -какое-нибудь решение уравнения (1).
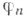 - полная система линейно независимых решений уравнения (1'), ck - произвольные постоянные. Сходные утверждения имеют место и для уравнения (2).
- полная система линейно независимых решений уравнения (1'), ck - произвольные постоянные. Сходные утверждения имеют место и для уравнения (2).
Пусть Т - непрерывный линейный оператор, отображающий банахово пространство Ев себя; Е*, Т* - соответствующие сопряженные пространство и оператор. Рассматриваются уравнения:
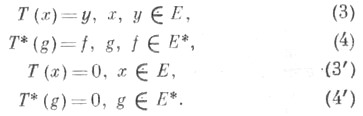
Справедливость Ф. <а. для оператора . означает следующее: 1) либо уравнения (3) и (4) разрешимы, каковы бы ни были их правые части, и тогда их решения единственны; 2) либо однородные уравнения (3') и (4') имеют одинаковое конечное число линейно независимых решений x1, ..., х п и g1, ..., gn соответственно; в этом случае для разрешимости уравнения (3) соответственно уравнения (4), необходимо и достаточно, чтобы gk (у)= 0, k= 1, 2, .... n, соответственно f( х k) =0, k=1, 2, ...,n; при этом общее решение уравнения (3) дастся равенством

а общее решение уравнения (4) - равенством

где х* (соответственно g*) - какое-нибудь решение уравнения (3) (уравнения (4)), а с 1 . . ., с n - произвольные постоянные.
Каждое из следующих двух условий необходимо и достаточно, чтобы для оператора Тимела место Ф. а. 1) Оператор Тпредставим в форме
T=W+V, где W- оператор, имеющий двусторонний непрерывный обратный, а V - вполне непрерывный оператор, 2) оператор Тпредставим в форме T=W1+V1. где W1 -оператор, имеющий двусторонний непрерывный обратный, а V1 - конечномерный оператор.
Лит.:[1] Смирнов В. И., Курс высшей математики, т. 4, ч. 1, 6 изд., М., 1974: [2] Владимиров В. С., Уравнения математической физики, 4 изд., М., 1981; [3] Канторович Л. В., Акимов Г. П., Функциональный анализ, 2 изд., М., 1977.
В. В. Хведелидзе.

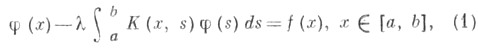

 каковы бы ни были известные функции f g, либо соответствующие однородные уравнения
каковы бы ни были известные функции f g, либо соответствующие однородные уравнения 

 -полная система линейно независимых решений уравнения (2'). При этом общее решение уравнения (1) имеет вид
-полная система линейно независимых решений уравнения (2'). При этом общее решение уравнения (1) имеет вид 

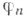 - полная система линейно независимых решений уравнения (1'), ck - произвольные постоянные. Сходные утверждения имеют место и для уравнения (2).
- полная система линейно независимых решений уравнения (1'), ck - произвольные постоянные. Сходные утверждения имеют место и для уравнения (2).