" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ

Значение ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ в математической энциклопедии:

производная многочлена, рациональной функции или формального степенного ряда, определяемая чисто алгебраически (без использования понятия предельного перехода) и имеющая смысл для любого кольца коэффициентов. Для многочлена

(или степенного ряда
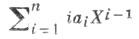Ф. п. F'(X)определяется как (соответственно как а для рациональной функции f(X) = P(X)/Q (Х)-эторациональная функция

Аналогично определяются Ф. п. высших порядков и частные Ф. п, для функций от нескольких переменных.
Для Ф. п, остается справедливым ряд свойств обычной производной. Так, если F' (Х)=0,то F(X)- константа из поля коэффициентов (в случае характеристики 0) и равна G(X^P) (в случае характеристики р). Если x₀ - корень многочлена кратности k, то х ₀ является корнем производной F'(X)кратности k-1.

Л. В. Кузьмин.