"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФИНСЛЕРОВА ГЕОМЕТРИЯ
Значение ФИНСЛЕРОВА ГЕОМЕТРИЯ в математической энциклопедии:
- метрическое обобщение римановой геометрии, возникающее вслед за введением общего определения длины вектора, не ограниченного частным римановым определением в виде корня квадратного из квадратичной формы. Развитие такого обобщения начинается с работы П. Финслера [1].
Предметом изучения в Ф. г. является действительное N-мерное дифференцируемое многообразие М(по меньшей мере класса C3) с системой локальных координат xi, на к-ром задана действительная неотрицательная скалярная функция F( х, у )от 2Nнезависимых переменных xi п yi, где у i- компоненты контравариантных векторов, касательных к Ми опирающихся на точку х i. Пусть F( х, у) принадлежит классу С 3по хi. и пусть в каждом касательном к Мпространстве М x существует такая область М * х,что, во-первых, она является конической (в том смысле, что если какой-либо вектор у i, опирающийся на нек-рую точку х i, принадлежит M*x, то M*x принадлежит и любой другой касательный вектор, коллинеарный у i иопирающийся на ту же точку х i),и, вo-вторых, F( х, у )принадлежит классу С 5 по  Ненулевые векторы
Ненулевые векторы  наз. допустимыми. Пусть, далее, для любого допустимого у i и любой точки х i справедливо:
наз. допустимыми. Пусть, далее, для любого допустимого у i и любой точки х i справедливо:

а также пусть функция F( х, у )положительно однородна первой степени по у i, т. е. F( х,ky)=kF( х, у) при любом k>0 для всех х i и допустимых у i. При этих условиях тройка ( М, M*x, F( х, у)) наз. N-мерным финслеровым пространством, a F- финслеровой метрической функцией. Значение функции F( х, у )понимается как длина вектора yi, опирающегося на точку х i.
Если финслерово пространство допускает такую координатную систему х i, что Fне зависит от этих х, то оно наз. пространством Минковского. Последнее находится в таком же отношении к финслерову пространству, в каком евклидово пространство к риманову пространству. Финслерово пространство называется положительно определенным, если на Fналожены условия, обеспечивающие положительную определенность квадратичной формы  при любых х i и ненулевых у i.
при любых х i и ненулевых у i.
Наложение условия однородности на . по у i имеет ясный геометрич. смысл с точки зрения инвариантных понятий, имеющихся в центроаффинных пространствах, каковыми являются касательные пространства М х. Именно, отношение длин любых двух коллинеарных векторов  из М * х может быть инвариантно определено следующим образом:
из М * х может быть инвариантно определено следующим образом: что не включает никакой метрич. функции. Таким образом, наложенное на F условие однородности является условием согласованности финслерова определения длины с частным центроаффинным определением; финслерова метрич. функция требуется для сравнения длин неколлицеарных векторов.
что не включает никакой метрич. функции. Таким образом, наложенное на F условие однородности является условием согласованности финслерова определения длины с частным центроаффинным определением; финслерова метрич. функция требуется для сравнения длин неколлицеарных векторов.
Тензор  наз. финслеровым метрическим тензором. В силу теорем Эйлера об однородных функциях
наз. финслеровым метрическим тензором. В силу теорем Эйлера об однородных функциях
 где, по определению, yi=gij(x,у) у i. Эти формулы представляют собой непосредственное обобщение своих риманоных аналогов, вытекающее из одного лишь условия однородности. Ф. г. сводится к римановой в случае, когда метрич. тензор gij(x, у )предполагается не зависящим от у n. Последнее условие можно записать в виде Cijk =0, где
где, по определению, yi=gij(x,у) у i. Эти формулы представляют собой непосредственное обобщение своих риманоных аналогов, вытекающее из одного лишь условия однородности. Ф. г. сводится к римановой в случае, когда метрич. тензор gij(x, у )предполагается не зависящим от у n. Последнее условие можно записать в виде Cijk =0, где

наз. картановским тензором кручения. Он удовлетворяет тождеству yiCijk = 0. Все финслеровы соотношения переходят в свои римановы аналоги при обращении в нуль тензора Cijk. Символы Кристоффеля  построенные по финслерову метрическому тензору по той же формуле, что и в римановой геометрии, не подчиняются закону преобразования коэффициентов связности. Тем не менее из первых производных от финслерова метрич. тензора можно построить коэффициенты связности такие, что (как и в римановой геометрии) ковариантная производная от метрич. тензора будет обращаться в нуль. Они наз. картановскими коэффициентами связности и имеют вид
построенные по финслерову метрическому тензору по той же формуле, что и в римановой геометрии, не подчиняются закону преобразования коэффициентов связности. Тем не менее из первых производных от финслерова метрич. тензора можно построить коэффициенты связности такие, что (как и в римановой геометрии) ковариантная производная от метрич. тензора будет обращаться в нуль. Они наз. картановскими коэффициентами связности и имеют вид

где

Из коммутаторов различных ковариантных производных находятся выражения финслеровых тензоров кривизны.
В каждом касательном пространстве М х финслерова метрич. функция определяет (N-1)-мерную гиперповерхность F( х, у)=-1(где х i рассматриваются фиксированными, у i -произвольными), наз. индикатрисой. Индикатриса образуется концами единичных касательных векторов li =yi/F(x,у). опирающихся на точку х i. Фундаментальное значение понятия индикатрисы видно уже из того, что вследствие однородности финслеровой метрич. функции индикатриса в точке х i однозначно определяет вид финслеровой метрич. функции F( х, у )в этой точке х i. В римановом случае индикатрисой является сфера. Вообще говоря, индикатрисой финслерова пространства может быть поверхность довольно общего вида. Финслеров метрич. тензор индуцирует на индикатрисе риманову метрику, превращая ее в риманово пространство. При каждом фиксированном хфинслеров метрич. тензор является римановым по переменным у. Пара  где х n фиксированы, а у n переменны, наз. касательным римановым пространством в точке х(евклидово пространство в случае римановой геометрии); риманов тензор кривизны этого пространства сводится к выражению
где х n фиксированы, а у n переменны, наз. касательным римановым пространством в точке х(евклидово пространство в случае римановой геометрии); риманов тензор кривизны этого пространства сводится к выражению  Индикатриса является гиперповерхностью, вложенной в касательное риманово пространство. Ближайшим примером финслеровой метрич. функции является корень f-й степени из формы f-го порядка.
Индикатриса является гиперповерхностью, вложенной в касательное риманово пространство. Ближайшим примером финслеровой метрич. функции является корень f-й степени из формы f-го порядка.
Пусть f(х)и rA (х)-действительные скалярные функции класса С 3, в каждой точке xудовлетворяющие условиям  и
и  суть N линейно независимых действительных ковариантных векторных полей класса С 3, А =1,2, ..., N. Тогда для
суть N линейно независимых действительных ковариантных векторных полей класса С 3, А =1,2, ..., N. Тогда для
 кривизна индикатрисы постоянна и равна f2/4(f-1), а для
кривизна индикатрисы постоянна и равна f2/4(f-1), а для

тензор кривизны индикатрисы равен нулю. Определитель финслерова метрич. тензора не зависит от yi тогда и только тогда, когда С i= 0, где  Если финслерово пространство положительно определено и индикатриса- выпуклая поверхность, то
Если финслерово пространство положительно определено и индикатриса- выпуклая поверхность, то  Функция F2 -единственный известный (1984) пример финслеровой метрич. функции, для к-рой С i=0 (не считая собственно риманова случая).
Функция F2 -единственный известный (1984) пример финслеровой метрич. функции, для к-рой С i=0 (не считая собственно риманова случая).
Можно выделять специальные типы финслеровых пространств, постулируя какой-либо специальный вид характерных финслеровых тензоров. Если основное многообразие Мдопускает иоле реперов 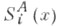 глобально, a F*( у А) - метрич. функция какого-либо пространства Минковского, то на Мможно ввести финслерову метрич. функцию:
глобально, a F*( у А) - метрич. функция какого-либо пространства Минковского, то на Мможно ввести финслерову метрич. функцию:

В этом случае финслерово пространство и метрич. функция наз. 1-формовыми. Функции F1 и F2 являются 1-формовыми, когда f и f А константы. Пространства 1-формовые можно считать наиболее простыми с точки зрения способа вхождения переменных х п в метрич. функцию. Финслерово пространство наз. С- сводимым, если оно не является римановым, N>2 и картановский тензор кручения представляется в виде

где hij = gij-lilj. Пространства С-сводймые могут иметь метрич. функции только двух типов: либо метрич. функцию Кропиной  либо метрич. функцию Рандерса
либо метрич. функцию Рандерса  где
где  bi (х)-ковариантное векторное поле, а ij (х) - риманов метрич. тензор. Напр., функция Лагранжа пробного электрич. заряда в гравитационном и электромагнитном полях является функцией Рандерса. Финслеров метрич. тензор, отвечающий функции F2, имеет сигнатуру (+ - - ...), что делает ее интересной для развития финслерова обобщения общей теории относительности; такая сигнатура встречается и в случае выбора метрич. функций вида F1. Такое обобщение можно основывать на концепции соприкосновения риманова пространства финслеровым, согласно к-рой каждому векторному полю у i (х)финслеров метрич. тензор ставит в соответствие т. н. соприкасающийся риманон метрич. тензор gmn(x,y(x)). Выделяя зависящие только от х i тензорные поля zA (х), из к-рых строится финслерова метрич. функция согласно F( х, у)=v(zA(x),yi. где v-скалярная функция, можно трактовать zA как собственно гравитационные полевые переменные. Финслерова геометризация пространства-времени дает также возможность развивать теорию физич. полей с различными внутренними симметриями, опираясь на понятие группы преобразований касательных векторов у i, оставляющих инвариантной финслерову метрич. функцию.
bi (х)-ковариантное векторное поле, а ij (х) - риманов метрич. тензор. Напр., функция Лагранжа пробного электрич. заряда в гравитационном и электромагнитном полях является функцией Рандерса. Финслеров метрич. тензор, отвечающий функции F2, имеет сигнатуру (+ - - ...), что делает ее интересной для развития финслерова обобщения общей теории относительности; такая сигнатура встречается и в случае выбора метрич. функций вида F1. Такое обобщение можно основывать на концепции соприкосновения риманова пространства финслеровым, согласно к-рой каждому векторному полю у i (х)финслеров метрич. тензор ставит в соответствие т. н. соприкасающийся риманон метрич. тензор gmn(x,y(x)). Выделяя зависящие только от х i тензорные поля zA (х), из к-рых строится финслерова метрич. функция согласно F( х, у)=v(zA(x),yi. где v-скалярная функция, можно трактовать zA как собственно гравитационные полевые переменные. Финслерова геометризация пространства-времени дает также возможность развивать теорию физич. полей с различными внутренними симметриями, опираясь на понятие группы преобразований касательных векторов у i, оставляющих инвариантной финслерову метрич. функцию.
Лит.:[1] Fins1еr P., Uber Kurven und Flachen in allgemeinen Raumen, Gott., 1918 (Diss.): [2] Рунд Х., Дифференциальная геометрия финслеровых пространств, пер. с англ., М., 1981; [3] Asanоv G. S., Finslerian Extension of General Relativity, Dordrecht, 1984.
Г. С. Асанов.

 Ненулевые векторы
Ненулевые векторы  наз. допустимыми. Пусть, далее, для любого допустимого у i и любой точки х i справедливо:
наз. допустимыми. Пусть, далее, для любого допустимого у i и любой точки х i справедливо: 
 при любых х i и ненулевых у i.
при любых х i и ненулевых у i.  из М * х может быть инвариантно определено следующим образом:
из М * х может быть инвариантно определено следующим образом: что не включает никакой метрич. функции. Таким образом, наложенное на F условие однородности является условием согласованности финслерова определения длины с частным центроаффинным определением; финслерова метрич. функция требуется для сравнения длин неколлицеарных векторов.
что не включает никакой метрич. функции. Таким образом, наложенное на F условие однородности является условием согласованности финслерова определения длины с частным центроаффинным определением; финслерова метрич. функция требуется для сравнения длин неколлицеарных векторов.  наз. финслеровым метрическим тензором. В силу теорем Эйлера об однородных функциях
наз. финслеровым метрическим тензором. В силу теорем Эйлера об однородных функциях  где, по определению, yi=gij(x,у) у i. Эти формулы представляют собой непосредственное обобщение своих риманоных аналогов, вытекающее из одного лишь условия однородности. Ф. г. сводится к римановой в случае, когда метрич. тензор gij(x, у )предполагается не зависящим от у n. Последнее условие можно записать в виде Cijk =0, где
где, по определению, yi=gij(x,у) у i. Эти формулы представляют собой непосредственное обобщение своих риманоных аналогов, вытекающее из одного лишь условия однородности. Ф. г. сводится к римановой в случае, когда метрич. тензор gij(x, у )предполагается не зависящим от у n. Последнее условие можно записать в виде Cijk =0, где 
 построенные по финслерову метрическому тензору по той же формуле, что и в римановой геометрии, не подчиняются закону преобразования коэффициентов связности. Тем не менее из первых производных от финслерова метрич. тензора можно построить коэффициенты связности такие, что (как и в римановой геометрии) ковариантная производная от метрич. тензора будет обращаться в нуль. Они наз. картановскими коэффициентами связности и имеют вид
построенные по финслерову метрическому тензору по той же формуле, что и в римановой геометрии, не подчиняются закону преобразования коэффициентов связности. Тем не менее из первых производных от финслерова метрич. тензора можно построить коэффициенты связности такие, что (как и в римановой геометрии) ковариантная производная от метрич. тензора будет обращаться в нуль. Они наз. картановскими коэффициентами связности и имеют вид 

 где х n фиксированы, а у n переменны, наз. касательным римановым пространством в точке х(евклидово пространство в случае римановой геометрии); риманов тензор кривизны этого пространства сводится к выражению
где х n фиксированы, а у n переменны, наз. касательным римановым пространством в точке х(евклидово пространство в случае римановой геометрии); риманов тензор кривизны этого пространства сводится к выражению  Индикатриса является гиперповерхностью, вложенной в касательное риманово пространство. Ближайшим примером финслеровой метрич. функции является корень f-й степени из формы f-го порядка.
Индикатриса является гиперповерхностью, вложенной в касательное риманово пространство. Ближайшим примером финслеровой метрич. функции является корень f-й степени из формы f-го порядка.  и
и  суть N линейно независимых действительных ковариантных векторных полей класса С 3, А =1,2, ..., N. Тогда для
суть N линейно независимых действительных ковариантных векторных полей класса С 3, А =1,2, ..., N. Тогда для  кривизна индикатрисы постоянна и равна f2/4(f-1), а для
кривизна индикатрисы постоянна и равна f2/4(f-1), а для 
 Если финслерово пространство положительно определено и индикатриса- выпуклая поверхность, то
Если финслерово пространство положительно определено и индикатриса- выпуклая поверхность, то  Функция F2 -единственный известный (1984) пример финслеровой метрич. функции, для к-рой С i=0 (не считая собственно риманова случая).
Функция F2 -единственный известный (1984) пример финслеровой метрич. функции, для к-рой С i=0 (не считая собственно риманова случая). 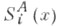 глобально, a F*( у А) - метрич. функция какого-либо пространства Минковского, то на Мможно ввести финслерову метрич. функцию:
глобально, a F*( у А) - метрич. функция какого-либо пространства Минковского, то на Мможно ввести финслерову метрич. функцию: 

 либо метрич. функцию Рандерса
либо метрич. функцию Рандерса  где
где  bi (х)-ковариантное векторное поле, а ij (х) - риманов метрич. тензор. Напр., функция Лагранжа пробного электрич. заряда в гравитационном и электромагнитном полях является функцией Рандерса. Финслеров метрич. тензор, отвечающий функции F2, имеет сигнатуру (+ - - ...), что делает ее интересной для развития финслерова обобщения общей теории относительности; такая сигнатура встречается и в случае выбора метрич. функций вида F1. Такое обобщение можно основывать на концепции соприкосновения риманова пространства финслеровым, согласно к-рой каждому векторному полю у i (х)финслеров метрич. тензор ставит в соответствие т. н. соприкасающийся риманон метрич. тензор gmn(x,y(x)). Выделяя зависящие только от х i тензорные поля zA (х), из к-рых строится финслерова метрич. функция согласно F( х, у)=v(zA(x),yi. где v-скалярная функция, можно трактовать zA как собственно гравитационные полевые переменные. Финслерова геометризация пространства-времени дает также возможность развивать теорию физич. полей с различными внутренними симметриями, опираясь на понятие группы преобразований касательных векторов у i, оставляющих инвариантной финслерову метрич. функцию.
bi (х)-ковариантное векторное поле, а ij (х) - риманов метрич. тензор. Напр., функция Лагранжа пробного электрич. заряда в гравитационном и электромагнитном полях является функцией Рандерса. Финслеров метрич. тензор, отвечающий функции F2, имеет сигнатуру (+ - - ...), что делает ее интересной для развития финслерова обобщения общей теории относительности; такая сигнатура встречается и в случае выбора метрич. функций вида F1. Такое обобщение можно основывать на концепции соприкосновения риманова пространства финслеровым, согласно к-рой каждому векторному полю у i (х)финслеров метрич. тензор ставит в соответствие т. н. соприкасающийся риманон метрич. тензор gmn(x,y(x)). Выделяя зависящие только от х i тензорные поля zA (х), из к-рых строится финслерова метрич. функция согласно F( х, у)=v(zA(x),yi. где v-скалярная функция, можно трактовать zA как собственно гравитационные полевые переменные. Финслерова геометризация пространства-времени дает также возможность развивать теорию физич. полей с различными внутренними симметриями, опираясь на понятие группы преобразований касательных векторов у i, оставляющих инвариантной финслерову метрич. функцию.