"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФИЛЬТРЗначение ФИЛЬТР в математической энциклопедии:
дуальный идеал,- непустое подмножество Fчастично упорядоченного множества Р, удовлетворяющее условиям: а) если  и нижняя грань inf {а, b} существует, то и нижняя грань inf {а, b} существует, то  б) если б) если  и и  то то  Понятие Ф. является двойственным к понятию идеала частично упорядоченного множества. Понятие Ф. является двойственным к понятию идеала частично упорядоченного множества.
Фильтром над нeпустым множеством Е (или в множестве Е)наз. собственный Ф. частично упорядоченного (относительно включения) множества подмножеств множества Е, т. е. любая непустая совокупность Fподмножеств множества Е, удовлетворяющая условиям: если  то то 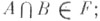 если если  и и  то то  пустое подмножество не принадлежит F. пустое подмножество не принадлежит F.
Базой фильтра наз. система подмножеств множества Е, удовлетворяющая двум условиям: 1) пустое множество ей не принадлежит; 2) пересечение двух принадлежащих ей подмножеств содержит нек-рое третье принадлежащее ей подмножество. Каждый Ф. полностью определяется любой из своих баз. Система всех подмножеств множества Е, каждое из к-рых содержит какой-нибудь элемент базы Ф., есть Ф. Он наз. натянутым на эту базу.
Множество всех Ф. над данным множеством частично упорядочено по включению. Максимальный элемент его наз. ультрафильтром (ультрафильтром наз. также максимальный собственный Ф. в любой булевой алгебре).
Примеры Ф. 1) Пусть Nk - подмножество натуральных чисел, кратных натуральному числу k;система {Nk:А=1, 2, . . .} есть база Ф.; натянутый на эту базу Ф. состоит из подмножеств, каждое из к-рых содержит нек-рое подмножество Nk.2) Совокупность всех подмножеств, содержащих любое непустое фиксированное подмножество  является Ф. над Е, называемым главным фильтром. Все Ф.. над конечными множествами - главные. 3) Если Е - бесконечное множество мощности является Ф. над Е, называемым главным фильтром. Все Ф.. над конечными множествами - главные. 3) Если Е - бесконечное множество мощности  ц F- совокупность "всех подмножеств множества Е, дополнения к-рых имеют мощность меньше ц F- совокупность "всех подмножеств множества Е, дополнения к-рых имеют мощность меньше  то Fявляется Ф. (он наз. фильтром Фреше). Фильтр Фреше - пример неглавного Ф. 4) Система подмножеств, содержащих нек-рую фиксированную точку множества, тоже есть Ф., более того, это - ультрафильтр. 5) Пусть на множестве Езадана топология, тогда окрестности любой точки то Fявляется Ф. (он наз. фильтром Фреше). Фильтр Фреше - пример неглавного Ф. 4) Система подмножеств, содержащих нек-рую фиксированную точку множества, тоже есть Ф., более того, это - ультрафильтр. 5) Пусть на множестве Езадана топология, тогда окрестности любой точки 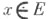 образуют Ф. образуют Ф. Лит.:[1] Б у р б а к и Н., Общая топология. Основные структуры, пер. с франц., М., 1968; [2] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [З] Мальце в А. И., Алгебраические системы, М., 1970.
В. И. Малыхин, Т. С. Фофанова.
|

 и нижняя грань inf {а, b} существует, то
и нижняя грань inf {а, b} существует, то  б) если
б) если  и
и  то
то  Понятие Ф. является двойственным к понятию идеала частично упорядоченного множества.
Понятие Ф. является двойственным к понятию идеала частично упорядоченного множества.  то
то 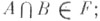 если
если  и
и  то
то  пустое подмножество не принадлежит F.
пустое подмножество не принадлежит F.  является Ф. над Е, называемым главным фильтром. Все Ф.. над конечными множествами - главные. 3) Если Е - бесконечное множество мощности
является Ф. над Е, называемым главным фильтром. Все Ф.. над конечными множествами - главные. 3) Если Е - бесконечное множество мощности  ц F- совокупность "всех подмножеств множества Е, дополнения к-рых имеют мощность меньше
ц F- совокупность "всех подмножеств множества Е, дополнения к-рых имеют мощность меньше  то Fявляется Ф. (он наз. фильтром Фреше). Фильтр Фреше - пример неглавного Ф. 4) Система подмножеств, содержащих нек-рую фиксированную точку множества, тоже есть Ф., более того, это - ультрафильтр. 5) Пусть на множестве Езадана топология, тогда окрестности любой точки
то Fявляется Ф. (он наз. фильтром Фреше). Фильтр Фреше - пример неглавного Ф. 4) Система подмножеств, содержащих нек-рую фиксированную точку множества, тоже есть Ф., более того, это - ультрафильтр. 5) Пусть на множестве Езадана топология, тогда окрестности любой точки 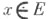 образуют Ф.
образуют Ф.