|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФЕРРАРИ МЕТОДЗначение ФЕРРАРИ МЕТОД в математической энциклопедии: - метод сведения решения уравнения 4-й степени к решению одного кубического и двух квадратных уравнений; найден Л. Феррари (L. Ferrari, опубл. 1545). Ф. м. для уравнения y4 + ay3 + by2 + cy + d =0 состоит в следующем. При помощи подстановки у=
Затем подбирается значение
Пусть
Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975. |
|
|
|

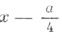 данное уравнение приводится к уравнению
данное уравнение приводится к уравнению 
 левую часть уравнения (1) можно преобразовать по формуле
левую часть уравнения (1) можно преобразовать по формуле 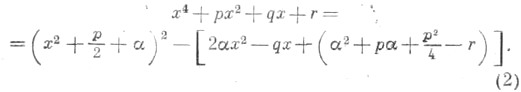
 так, чтобы выражение в квадратных скобках было полным квадратом. Для этого нужно, чтобы дискриминант квадратного трехчлена был равен нулю. Это дает для
так, чтобы выражение в квадратных скобках было полным квадратом. Для этого нужно, чтобы дискриминант квадратного трехчлена был равен нулю. Это дает для  кубическое уравнение
кубическое уравнение 
 - один из корней этого уравнения. При
- один из корней этого уравнения. При  многочлен в квадратных скобках в (2) имеет один двукратный корень
многочлен в квадратных скобках в (2) имеет один двукратный корень