" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ФЕРМА ТЕОРЕМА

Значение ФЕРМА ТЕОРЕМА в математической энциклопедии:

- необходимое условие локального экстремума дифференцируемой функции. Пусть действительная функция f определена в окрестности точки 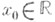и дифференцируема в этой точке. Тогда, если функция fимеет в точке х ₀ локальный экстремум, то ее производная в х ₀ равна нулю: f'(z₀)=0. Геометрически это означает, что касательная к графику функции f в точке (x₀, f(x₀)) горизонтальна. Впервые равносильное условие для экстремумов многочленов было получено П. Ферма (P. Fermat) в 1629, но опубликовано лишь в 1679.

Л. Д. Кудрявцев.