"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФАКТОРИАЛЬНОЕ КОЛЬЦОЗначение ФАКТОРИАЛЬНОЕ КОЛЬЦО в математической энциклопедии:
- кольцо с однозначным разложением на множители. Точнее, Ф. к. А- это область целостности, в к-рой можно выбрать систему экстремальных элементов . такую, что любой ненулевой элемент  допускает единственное представление вида допускает единственное представление вида 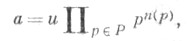
где иобратим, а целые неотрицательные показатели (р)отличны от нуля только для конечного числа элементов  При этом элемент наз. экстремальным в А, если из p=uv следует, что либо и, либо vобратим в А, и р необратим в А. При этом элемент наз. экстремальным в А, если из p=uv следует, что либо и, либо vобратим в А, и р необратим в А.
В Ф. к. существует наибольший общий делитель и наименьшее общее кратное любых двух элементов. Кольцо Афакториально тогда и только тогда, когда оно является кольцом Крулля и выполняется одно из следующих эквивалентных условий: (1) любой диви-зориальный идеал в . является главным; (2) любой простой идеал высоты 1 главный; (3) любое непустое семейство главных идеалов обладает максимальным элементом, н пересечение любых двух главных идеалов является главным идеалом. Любое кольцо главных идеалов факторнально. Дедекиндово кольцо факториально, только если оно - кольцо главных идеалов. Если S - мультипликативная система в Ф. к. А, то кольцо частных S-1Aфакториально. Для кольца Зариского Rиз факториальности его пополнения Rследует факториальность самого R.
Подкольцо и факторкольцо Ф. к. не обязаны быть Ф. к. Кольцо многочленов над Ф. к. и кольцо формальных степенных рядов над полем или дискретно нормированным кольцом факториально. Однако кольцо формальных степенных рядов над Ф. к. не обязано быть факториальным.
Область целостности факториальна тогда и только тогда, когда ее мультипликативная полугруппа гауссова (см. Гауссова полугруппа), в связи с этим Ф. к, наз, также гауссовыми кольцами.
Лит.: [1] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971.
Л. В. Кузьмин.
|

 допускает единственное представление вида
допускает единственное представление вида 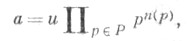
 При этом элемент наз. экстремальным в А, если из p=uv следует, что либо и, либо vобратим в А, и р необратим в А.
При этом элемент наз. экстремальным в А, если из p=uv следует, что либо и, либо vобратим в А, и р необратим в А.