"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
УСТОЙЧИВОСТЬ ХАРАКТЕРИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ
Значение УСТОЙЧИВОСТЬ ХАРАКТЕРИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ в математической энциклопедии:
- свойство Ляпунова характеристических показателей линейной системы обыкновенных дифференциальных уравнений
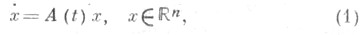
где 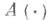 - непрерывное отображение
- непрерывное отображение 
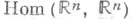 (или
(или  удовлетворяющее условию
удовлетворяющее условию
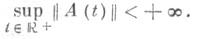
Говорят, что характеристич. показатели Ляпунова системы (1) устойчивы, если каждая из функций
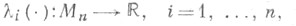
непрерывна в точке А. Здесь  - характеристич. показатели Ляпунова системы (1), a Mn - множество систем (1), наделенное структурой метрнч. пространства заданием расстояния
- характеристич. показатели Ляпунова системы (1), a Mn - множество систем (1), наделенное структурой метрнч. пространства заданием расстояния
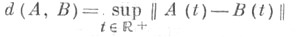
(для удобства система (1) отождествляется с отображением 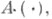 причем вместо
причем вместо 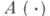 пишется А).
пишется А).
Были обнаружены (см. [2], [3]) системы (1) с неустойчивыми характеристич. показателями. Напр., характеристич. показатели системы .
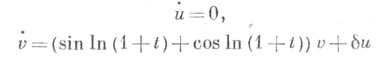
при 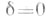 неустойчивы, т. к. при
неустойчивы, т. к. при  ее старший характеристич. показатель
ее старший характеристич. показатель 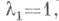 а при
а при 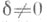 показатель
показатель  и не зависит от
и не зависит от 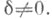 Для устойчивости характеристич. показателей достаточно, чтобы выполнялось интегральной разделенности условие (теорема Перрона). Множество систем (1), удовлетворяющих этому условию, совпадает с внутренностью (в пространстве М п )множества всех систем (1) с устойчивыми характеристич. показателями.
Для устойчивости характеристич. показателей достаточно, чтобы выполнялось интегральной разделенности условие (теорема Перрона). Множество систем (1), удовлетворяющих этому условию, совпадает с внутренностью (в пространстве М п )множества всех систем (1) с устойчивыми характеристич. показателями.
Если 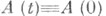 при всех
при всех  или A(t+T)=A(t)при всех
или A(t+T)=A(t)при всех  (при нек-ром T>0) (т. е. система (1) имеет постоянные или периодич. коэффициенты), то характеристич. показатели системы (1) устойчивы.
(при нек-ром T>0) (т. е. система (1) имеет постоянные или периодич. коэффициенты), то характеристич. показатели системы (1) устойчивы.
Если  - почтп периодич. отображение (см. Линейная система дифференциальных уравнений с почти периодическими коэффициентами),то для У. х. п. системы (1) необходимо и достаточно, чтобы система (1) была почти приводима.
- почтп периодич. отображение (см. Линейная система дифференциальных уравнений с почти периодическими коэффициентами),то для У. х. п. системы (1) необходимо и достаточно, чтобы система (1) была почти приводима.
Для того чтобы характеристич. показатели системы (1) были устойчивы, достаточно, чтобы нашлось Ляпунова преобразование, приводящее систему (1) к клеточно-диагональному виду
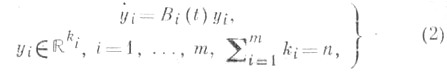
такому, что: а) клетки интегрально разделены, т. е. найдутся числа d>0, a>0 такие, что
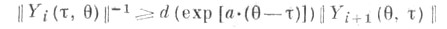
для всех 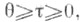 i=l, . . ., m-1 (здесь
i=l, . . ., m-1 (здесь 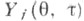 - Коши оператор системы (2)); б) верхний и нижним центральные показатели, системы (2) равны друг другу:
- Коши оператор системы (2)); б) верхний и нижним центральные показатели, системы (2) равны друг другу:
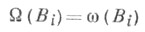 при всяком i = l, ..., m.
при всяком i = l, ..., m.
Условия этой теоремы являются и необходимыми условиями У. х. п. системы (1) (см. [6]). Системы с неустойчивыми характеристич. показателями могут обладать свойством стохастической У. х. п.
Характеристич. показатели системы (1) наз. стохастически устойчивыми (или устойчивыми почти наверное), если при  характеристич. показатели Ляпунова системы
характеристич. показатели Ляпунова системы
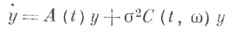
стремятся с вероятностью 1 к характеристич. показателям Ляпунова системы (1); здесь элементы матрицы, задающей линейные операторы 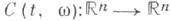 (в нек-ром- не зависящем от
(в нек-ром- не зависящем от 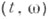 -базисе пространства
-базисе пространства 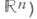 суть независимые ненулевые белые шумы.
суть независимые ненулевые белые шумы.
Если отображение 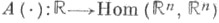 равномерно непрерывно и
равномерно непрерывно и

то для почти всякого отображения 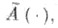 где
где
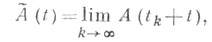
характеристич. показатели системы  стохастически устойчивы (для сдвигов динамической системы
стохастически устойчивы (для сдвигов динамической системы  рассматривают нормированную инвариантную меру, сосредоточенную на замыкании траектории точки
рассматривают нормированную инвариантную меру, сосредоточенную на замыкании траектории точки  под почти всяким
под почти всяким  понимается почти всякое
понимается почти всякое  в смысле всякой такой меры). Пусть динамич. система на гладком замкнутом многообразии Vn задана гладким векторным полем. Тогда для почтп всякой (в смысле всякой нормированной инвариантной меры) точки
в смысле всякой такой меры). Пусть динамич. система на гладком замкнутом многообразии Vn задана гладким векторным полем. Тогда для почтп всякой (в смысле всякой нормированной инвариантной меры) точки  характеристич. показатели системы уравнений в вариациях вдоль траектории точки хстохастически устойчивы.
характеристич. показатели системы уравнений в вариациях вдоль траектории точки хстохастически устойчивы.
Лит.:[1] Ляпунов А. М., Собр. соч. т. 2 М.- Л. 1956; [2]Perron О., лMath. Z.

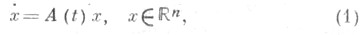
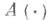 - непрерывное отображение
- непрерывное отображение 
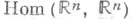 (или
(или  удовлетворяющее условию
удовлетворяющее условию 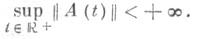
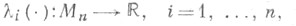
 - характеристич. показатели Ляпунова системы (1), a Mn - множество систем (1), наделенное структурой метрнч. пространства заданием расстояния
- характеристич. показатели Ляпунова системы (1), a Mn - множество систем (1), наделенное структурой метрнч. пространства заданием расстояния 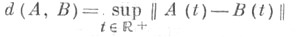
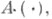 причем вместо
причем вместо 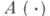 пишется А).
пишется А). 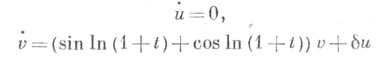
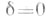 неустойчивы, т. к. при
неустойчивы, т. к. при  ее старший характеристич. показатель
ее старший характеристич. показатель 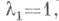 а при
а при 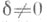 показатель
показатель  и не зависит от
и не зависит от 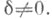 Для устойчивости характеристич. показателей достаточно, чтобы выполнялось интегральной разделенности условие (теорема Перрона). Множество систем (1), удовлетворяющих этому условию, совпадает с внутренностью (в пространстве М п )множества всех систем (1) с устойчивыми характеристич. показателями.
Для устойчивости характеристич. показателей достаточно, чтобы выполнялось интегральной разделенности условие (теорема Перрона). Множество систем (1), удовлетворяющих этому условию, совпадает с внутренностью (в пространстве М п )множества всех систем (1) с устойчивыми характеристич. показателями. 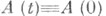 при всех
при всех  или A(t+T)=A(t)при всех
или A(t+T)=A(t)при всех  (при нек-ром T>0) (т. е. система (1) имеет постоянные или периодич. коэффициенты), то характеристич. показатели системы (1) устойчивы.
(при нек-ром T>0) (т. е. система (1) имеет постоянные или периодич. коэффициенты), то характеристич. показатели системы (1) устойчивы.  - почтп периодич. отображение (см. Линейная система дифференциальных уравнений с почти периодическими коэффициентами),то для У. х. п. системы (1) необходимо и достаточно, чтобы система (1) была почти приводима.
- почтп периодич. отображение (см. Линейная система дифференциальных уравнений с почти периодическими коэффициентами),то для У. х. п. системы (1) необходимо и достаточно, чтобы система (1) была почти приводима. 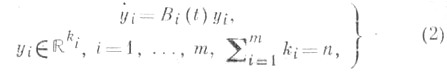
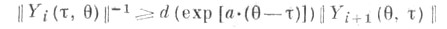
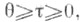 i=l, . . ., m-1 (здесь
i=l, . . ., m-1 (здесь 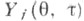 - Коши оператор системы (2)); б) верхний и нижним центральные показатели, системы (2) равны друг другу:
- Коши оператор системы (2)); б) верхний и нижним центральные показатели, системы (2) равны друг другу: 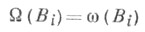 при всяком i = l, ..., m.
при всяком i = l, ..., m.  характеристич. показатели Ляпунова системы
характеристич. показатели Ляпунова системы 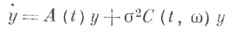
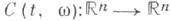 (в нек-ром- не зависящем от
(в нек-ром- не зависящем от 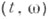 -базисе пространства
-базисе пространства 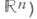 суть независимые ненулевые белые шумы.
суть независимые ненулевые белые шумы. 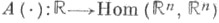 равномерно непрерывно и
равномерно непрерывно и 
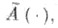 где
где 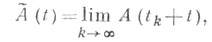
 стохастически устойчивы (для сдвигов динамической системы
стохастически устойчивы (для сдвигов динамической системы  рассматривают нормированную инвариантную меру, сосредоточенную на замыкании траектории точки
рассматривают нормированную инвариантную меру, сосредоточенную на замыкании траектории точки  под почти всяким
под почти всяким  понимается почти всякое
понимается почти всякое  в смысле всякой такой меры). Пусть динамич. система на гладком замкнутом многообразии Vn задана гладким векторным полем. Тогда для почтп всякой (в смысле всякой нормированной инвариантной меры) точки
в смысле всякой такой меры). Пусть динамич. система на гладком замкнутом многообразии Vn задана гладким векторным полем. Тогда для почтп всякой (в смысле всякой нормированной инвариантной меры) точки  характеристич. показатели системы уравнений в вариациях вдоль траектории точки хстохастически устойчивы.
характеристич. показатели системы уравнений в вариациях вдоль траектории точки хстохастически устойчивы.