"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ
Значение УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ в математической энциклопедии:
1) У. у. с.-свойство упругих систем (упругих тел или совокупностей взаимодействующих упругих тел) мало отклоняться от состояния равновесия (движения) при достаточно малых возмущающих воздействиях. Роль возмущающих воздействий играют флуктуации внешних сил, отклонения от идеальной геометрич. формы, дефекты материала и т. п.
2) У. у. с.- раздел механики деформируемого твердого тела, предметом к-рого является изучение У. у. с. В более широкой трактовке этот раздел включает изучение устойчивости вязко-упругих, упруго-пластических и др. деформируемых систем; часто употребляют также термин устойчивость деформируемых систем.
Понятие У. у. с. тесно связано с общим понятием устойчивости движения, в частности с понятием устойчивости по Ляпунову. Центральная задача теории У. у. с.- нахождение области в пространстве параметров системы и внешних воздействий, в пределах к-рой рассматриваемое состояние равновесия (движения) остается устойчивым. Поверхность, ограничивающая область устойчивости, наз. критической поверхностью. Часто воздействие на упругую систему задают с точностью до одного параметра  Без ограничения общности можно принять, что
Без ограничения общности можно принять, что  причем при
причем при  имеет место устойчивость. Нижняя грань
имеет место устойчивость. Нижняя грань  значений параметра
значений параметра 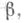 при к-рых исследуемое равновесие (движение) перестает быть устойчивым, наз. критическим параметром. Задачи У. у. с. имеют большое прикладное значение: потеря устойчивости элементов конструкций, машин и приборов, как правило, влечет утрату несущей способности или нарушение нормальных условий эксплуатации.
при к-рых исследуемое равновесие (движение) перестает быть устойчивым, наз. критическим параметром. Задачи У. у. с. имеют большое прикладное значение: потеря устойчивости элементов конструкций, машин и приборов, как правило, влечет утрату несущей способности или нарушение нормальных условий эксплуатации.
Строгая теория У. у. с. основана на распространении классич. устойчивости теории на континуальные системы и может рассматриваться как приложение теории дифференциальных уравнений в банаховом пространстве. Близость исследуемого состояния и возмущенных состояний оценивается по нек-рой норме. В практич. расчетах широко применяют аппроксимацию континуальных систем конечномерными системами с широким привлечением вариационных, сеточных и т. п. приближенных методов.
В случае упругой системы с идеальными связями, нагруженной потенциальными не зависящими от времени силами, система в целом консервативная. Условия устойчивости равновесия даются теоремой Лагранжа - Дирихле, согласно к-poй в положении устойчивого равновесия потенциальная анергия системы П имеет изолированный минимум. На этой теореме основан энергетический метод исследования У. у. с., состоящий в изучении изменения потенциальной энергии системы П при изменении параметров. При этом П [u] - функционал от поля перемещений и. В однопараметрич. задачах У. у. с. критич. параметр b* есть нижняя грань значений b, при к-рых нарушается неравенство 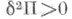 при условии
при условии  В окрестности критич. значений
В окрестности критич. значений  происходит бифуркация форм равновесия.
происходит бифуркация форм равновесия.
Для вычисления критич. параметров, отвечающих точкам бифуркации, вместо энергетич. метода обычно используют статический метод. При этом задача У. у. с. сводится к линейной задаче о собственных значениях для операторного уравнения, соответствующего вариационному условию  Здесь I[и] - квадратичный функционал от поля перемещений, к-рый формально совпадает с
Здесь I[и] - квадратичный функционал от поля перемещений, к-рый формально совпадает с  если вариацию
если вариацию  заменить на и. Минимальное собственное значение принимают за критич. параметр. Как правило, дополнительный анализ подтверждает, что при достижении минимального собственного значения происходит бифуркация форм равновесия.
заменить на и. Минимальное собственное значение принимают за критич. параметр. Как правило, дополнительный анализ подтверждает, что при достижении минимального собственного значения происходит бифуркация форм равновесия.
Оба метода берут начало от работ Л. Эйлера (L. Euler) по основам классич. вариационного исчисления (1744- 1757). Им же решены простейшие задачи об устойчивости призматич. упругих стержней при осевом сжатии, а также изучено поведение стержней после потери устойчивости. Для стержня, шарнирно опертого по концам, критич. сила равна

где Е - модуль Юнга материала, J - момент инерции поперечного сечения, l - длина стержня. Накоплено большое количество конкретных результатов для стержней, стержневых систем, пластин, оболочек, а также тел, все характерные размеры к-рых имеют одинаковый порядок (см. [1]).
В случае непотенциальных сил энергетич. и статич. методы, вообще говоря, неприменимы (см. 12]). Они неприменимы также в динамических задачах У. у. с. (см. [3]). Во всех этих случаях используют динамический метод, состоящий в рассмотрении малых движений системы в окрестности исследуемого равновесия (движения). При постоянных во времени внешних воздействиях изучение устойчивости сводится к обобщенной задаче о собственных значениях относительно параметров системы, а также характеристич. показателей или комплексных собственных частот. Динамич. метод основан на распространении теорем об устойчивости по первому приближению на континуальные системы. Если при постановке конкретной задачи не допущено переупрощений, то такой метод дает правильные результаты. В противном случае возможны явления, известные под названием парадоксов стабилизации и дестабилизации (см. [4]). Среди неконсервативных задач теории У. у. с. значительное место принадлежит задачам аэроупругости и гидроупругости (см. [2], [5], (6]), а также задачам устойчивости при периодических внешних воздействиях (см. [3]). Последние тесно связаны с теорией нараметрич. резонансов для континуальных систем.
Обобщение теории У. у. с. на упруго-пластические системы связано с преодолением серьезных трудностей исследования устойчивости существенно нелинейных неголономных континуальных систем (см. [7]). Для систем из материалов, подверженных ползучести и другим явлениям, протекающим во времени, требуется исследование устойчивости на конечном интервале времени [8].
Лит.:[1] Вольмир А. С., Устойчивость деформируемых систем, 2 изд.. М., 1967; [2] Болотин В. В., Неконсервативные задачи теории упругой устойчивости, М., 1961; [3] его же, Динамическая устойчивость упругих систем, М., 1956; [4] его же, в кн.: Проблемы устойчивости движения, аналитической механики и управления движением, Новосиб., 1979, с. 7-17; [5] Вольмир А. С., Оболочки в потоке жидкости и газа. Задачи аэроупругости, М., 1976; [6] его же, Оболочки в потоке жидкости и газа. Задачи гидроупругости, М., 1979; [7] Клюшников В. Д., Устойчивость упруго-пластических систем, М., 1980; [8] Работнов Ю. Н., Элементы наследственной механики твердых тел, М., 1977.
В. В. Болотин.

 Без ограничения общности можно принять, что
Без ограничения общности можно принять, что  причем при
причем при  имеет место устойчивость. Нижняя грань
имеет место устойчивость. Нижняя грань  значений параметра
значений параметра 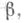 при к-рых исследуемое равновесие (движение) перестает быть устойчивым, наз. критическим параметром. Задачи У. у. с. имеют большое прикладное значение: потеря устойчивости элементов конструкций, машин и приборов, как правило, влечет утрату несущей способности или нарушение нормальных условий эксплуатации.
при к-рых исследуемое равновесие (движение) перестает быть устойчивым, наз. критическим параметром. Задачи У. у. с. имеют большое прикладное значение: потеря устойчивости элементов конструкций, машин и приборов, как правило, влечет утрату несущей способности или нарушение нормальных условий эксплуатации. 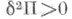 при условии
при условии  В окрестности критич. значений
В окрестности критич. значений  происходит бифуркация форм равновесия.
происходит бифуркация форм равновесия.  Здесь I[и] - квадратичный функционал от поля перемещений, к-рый формально совпадает с
Здесь I[и] - квадратичный функционал от поля перемещений, к-рый формально совпадает с  если вариацию
если вариацию  заменить на и. Минимальное собственное значение принимают за критич. параметр. Как правило, дополнительный анализ подтверждает, что при достижении минимального собственного значения происходит бифуркация форм равновесия.
заменить на и. Минимальное собственное значение принимают за критич. параметр. Как правило, дополнительный анализ подтверждает, что при достижении минимального собственного значения происходит бифуркация форм равновесия. 