"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
УСТОЙЧИВОСТЬ ПО ЧАСТИ ПЕРЕМЕННЫХ
Значение УСТОЙЧИВОСТЬ ПО ЧАСТИ ПЕРЕМЕННЫХ в математической энциклопедии:
- устойчивость в смысле Ляпунова решения х=0по отношению не ко всем, а лишь к нек-рым переменным x1, . . .. xk, k< п, системы обыкновенных дифференциальных уравнений
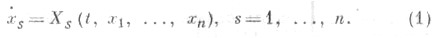
Здесь Xs(t, x)- данные действительные непрерывные функции, удовлетворяющие в области

условиям существования и единственности решения x(t; t0, х 0), причем Xs(t, 0)=0, s = l, ..., n, и любое решение определено для всех 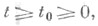 при к-рых
при к-рых 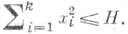
Пусть xi = yi при i =1, . . ., k; xk+j = zj при j =1, ... ..., т, n = k+m и 
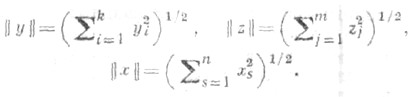
Решение х=0системы (1) наз.:
а) устойчивым по отношению к x1,..., х k, или y-устойчивым, если
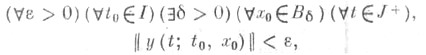
т. e. при всяких произвольно задаваемых числах 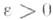
 и
и  найдется число
найдется число  такое, что при всяких возмущениях x0, удовлетворяющих условию
такое, что при всяких возмущениях x0, удовлетворяющих условию  и при всяком t>t0 для решении x(t; t0, х 0) выполняется условие
и при всяком t>t0 для решении x(t; t0, х 0) выполняется условие 
б) y-нeустоичивым в противном случаи, т. е. если
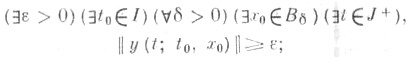
в) у- устойчивым равномерно по t0, если в определении а) для каждого 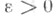 число
число 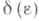 можно выбрать не зависящим от t0;
можно выбрать не зависящим от t0;
г) асимптотически у- устойчивым, если оно y-устойчиво и для каждого 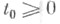 существует число
существует число 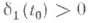 такое, что
такое, что

Здесь 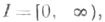 J+ -максимальный правый интервал, где х(t; t0, x0) определено,
J+ -максимальный правый интервал, где х(t; t0, x0) определено,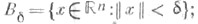 в случае г), кроме указанных выше условий, предполагается, что все решения системы (1) существуют на
в случае г), кроме указанных выше условий, предполагается, что все решения системы (1) существуют на 
Постановка задачи об У. по ч. н. дана Л. М. Ляпуновым [1] как обобщение задачи устойчивости по всем переменным (k=n). При решении этой задачи особенно эффективным оказался метод Ляпунова функции, модифицированный (см. [2]) применительно к задачам y-устойчивости. В основе метода лежит ряд теорем, обобщающих классич. теоремы Ляпунова.
Пусть рассматриваются действительные однозначные функции 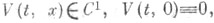 а также их полные производные по времени в силу (1):
а также их полные производные по времени в силу (1):

Знакопостоянная функция V(t, х )наз. у-знакоопределенной, если существует положительно-определенная функция W(y)такая, что в области (2)
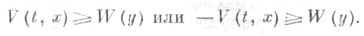
Ограниченная функция V(t, х )допускает бесконечно малый высший предел по х 1, . .., x р, если для всякого числа l>0 найдется 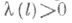 такое, что |V(t,x)|<l при
такое, что |V(t,x)|<l при 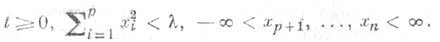
Теорема 1. Если система (1) такова, что существует y-положительно-определенная функция V(t, х), производная к-рой 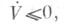 то решение х=0является y-устойчивым.
то решение х=0является y-устойчивым.
Теорема 2. Если выполнены условия теоремы 1 и, кроме того, V допускает бесконечно малый высший предел но х, то решение х=0 системы (1) y-устойчиво равномерно по t0.
Теорема 3. Если выполнены условия теоремы 1 и, кроме того, Vдопускает бесконечно малый высший предел по у, то для любого  найдется
найдется 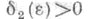 такое, что из
такое, что из 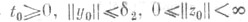 следует справедливость неравенства
следует справедливость неравенства 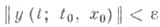 для всех
для всех 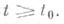
Теорема 4. Если система (1) такова, что существует y-положительно-определенная функция V, допускающая бесконечно малый высший предел по х 1, . . .., x р  производная к-рой V отрицательно-определенная но х 1, . . ., x р, то решение х=0системы (1) асимптотически y-устойчиво.
производная к-рой V отрицательно-определенная но х 1, . . ., x р, то решение х=0системы (1) асимптотически y-устойчиво.
Для исследования y-неустойчивости успешно применяются теорема о неустойчивости Четаева (см. Четчева функция). а также нек-рые другие теоремы. Установлены условия обратимости ряда теорем об y-устойчивости, напр. обратимость теорем 1, 2, а также теоремы 4 при p=k. Применяются методы дифференциальных неравенств и вектор-функций Ляпунова; установлены теоремы об асимптотической y-устойчивости в целом, но 1-му приближению и т. п. (см. [3]).
Лит.:[1] Ляпунов А. М., лМатем. сб.

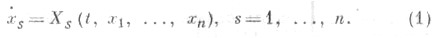

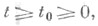 при к-рых
при к-рых 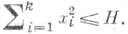

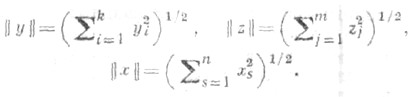
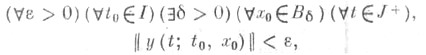
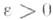
 и
и  найдется число
найдется число  такое, что при всяких возмущениях x0, удовлетворяющих условию
такое, что при всяких возмущениях x0, удовлетворяющих условию  и при всяком t>t0 для решении x(t; t0, х 0) выполняется условие
и при всяком t>t0 для решении x(t; t0, х 0) выполняется условие 
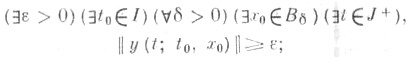
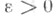 число
число 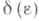 можно выбрать не зависящим от t0;
можно выбрать не зависящим от t0; 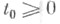 существует число
существует число 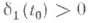 такое, что
такое, что 
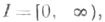 J+ -максимальный правый интервал, где х(t; t0, x0) определено,
J+ -максимальный правый интервал, где х(t; t0, x0) определено,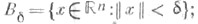 в случае г), кроме указанных выше условий, предполагается, что все решения системы (1) существуют на
в случае г), кроме указанных выше условий, предполагается, что все решения системы (1) существуют на 
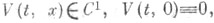 а также их полные производные по времени в силу (1):
а также их полные производные по времени в силу (1): 
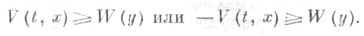
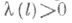 такое, что |V(t,x)|<l при
такое, что |V(t,x)|<l при 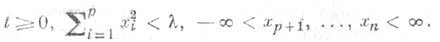
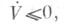 то решение х=0является y-устойчивым.
то решение х=0является y-устойчивым.  найдется
найдется 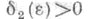 такое, что из
такое, что из 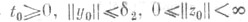 следует справедливость неравенства
следует справедливость неравенства 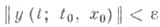 для всех
для всех 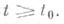
 производная к-рой V отрицательно-определенная но х 1, . . ., x р, то решение х=0системы (1) асимптотически y-устойчиво.
производная к-рой V отрицательно-определенная но х 1, . . ., x р, то решение х=0системы (1) асимптотически y-устойчиво.