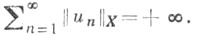"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
УСЛОВНАЯ СХОДИМОСТЬ
Значение УСЛОВНАЯ СХОДИМОСТЬ в математической энциклопедии:
ряда - свойство ряда, заключающееся в том, что существует сходящийся ряд, полученный из данного нек-рой перестановкой его членов. Числовой ряд

безусловно сходится, если он сходится, и сходится любой ряд, полученный перестановкой его членов, причем сумма любого такого ряда одна и та же, иначе говоря, сумма безусловно сходящегося ряда не зависит от порядка его членов. Если ряд (*) сходится, но не безусловно, то он наз. условно сходящимся. Для того чтобы ряд (*) условно сходился, необходимо и достаточно, чтобы он сходился, но не абсолютно, т. е. чтобы

Если члены ряда (*) являются действительными числами, через  обозначены его неотрицательные члены, а через
обозначены его неотрицательные члены, а через 
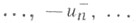 - отрицательные, то ряд (*) будет условно сходиться тогда и только тогда, когда оба ряда
- отрицательные, то ряд (*) будет условно сходиться тогда и только тогда, когда оба ряда  расходятся (при этом порядок слагаемых в этих рядах безразличен).
расходятся (при этом порядок слагаемых в этих рядах безразличен).
Пусть ряд (*) с действительными членами сходится условно и 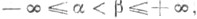 тогда существует такой ряд
тогда существует такой ряд 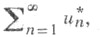 полученный перестановкой членов ряда (*), что если обозначить через
полученный перестановкой членов ряда (*), что если обозначить через 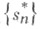 последовательность его частичных сумм, то
последовательность его частичных сумм, то

(это есть обобщение теоремы Римана).
Произведение условно сходящихся рядов зависит от порядка, в к-ром суммируются результаты почленного умножения членов данных рядов.
Понятие условной и безусловной сходимости ряда обобщается на ряды, члены к-рых являются элементами нек-рого нормированного векторного пространства X. Если X-конечномерное пространство, то аналогично случаю числовых рядов сходящийся ряд
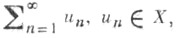 п =1, 2, ..., условно сходится тогда и только тогда, когда ряд
п =1, 2, ..., условно сходится тогда и только тогда, когда ряд  расходится. Если же пространство Xбесконечномерное, то в нем существуют безусловно сходящиеся ряды
расходится. Если же пространство Xбесконечномерное, то в нем существуют безусловно сходящиеся ряды 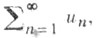 не являющиеся абсолютно сходящимися, т. е. такие, что для них
не являющиеся абсолютно сходящимися, т. е. такие, что для них
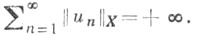
Л. Д. Кудрявцев.



 обозначены его неотрицательные члены, а через
обозначены его неотрицательные члены, а через 
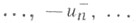 - отрицательные, то ряд (*) будет условно сходиться тогда и только тогда, когда оба ряда
- отрицательные, то ряд (*) будет условно сходиться тогда и только тогда, когда оба ряда  расходятся (при этом порядок слагаемых в этих рядах безразличен).
расходятся (при этом порядок слагаемых в этих рядах безразличен). 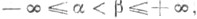 тогда существует такой ряд
тогда существует такой ряд 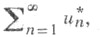 полученный перестановкой членов ряда (*), что если обозначить через
полученный перестановкой членов ряда (*), что если обозначить через 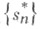 последовательность его частичных сумм, то
последовательность его частичных сумм, то 
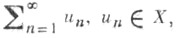 п =1, 2, ..., условно сходится тогда и только тогда, когда ряд
п =1, 2, ..., условно сходится тогда и только тогда, когда ряд  расходится. Если же пространство Xбесконечномерное, то в нем существуют безусловно сходящиеся ряды
расходится. Если же пространство Xбесконечномерное, то в нем существуют безусловно сходящиеся ряды 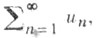 не являющиеся абсолютно сходящимися, т. е. такие, что для них
не являющиеся абсолютно сходящимися, т. е. такие, что для них