|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БРАНДТА ПОЛУГРУППАЗначение БРАНДТА ПОЛУГРУППА в математической энциклопедии: -полугруппа Sс нулем, в к-рой каждому ненулевому элементу асоответствуют такие однозначно определенные элементы Частичный группоид, получающийся выкидыванием нуля из Б. п., наз. группоидом Бранд-т а. Это понятие было введено Г. Брандтом в [1], фактически там же было введено понятие Б. п. Понятие группоида Брандта является абстракцией системы нормальных идеалов полупростых линейных алгебр относительно так наз. собственного умножения (см. [2], гл. 6, а также [3], гл. 6). Роль Б. п. для теории полугрупп определяется тем, что Б. п.- это в точности вполне 0-простые инверсные полугруппы (см. Вполне простая полугруппа). Полугруппа будет Б. п. тогда и только тогда, когда она изоморфна рисовской полугруппе матричного типа с единичной сэндвич-матрицей над группой с присоединенным нулем. Лит.:[1| Вrandt H., "Math, Ann.", 1927, Bd 96, S. 360-66; [2] Deurin g M., Algebren, В., 1935; [3] Джекобсон Н., Теория колец, пер. с англ., М., 1947; [4]Сушкевич А. К., Теория обобщенных групп, Хар.-К., 1937; [5] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972. Л. Н. Шеврин. |
|
|
|

 , что
, что  , и для любых двух ненулевых идемпотентов
, и для любых двух ненулевых идемпотентов  имеет место
имеет место  . Элементы е и/, указанные в определении, на самом деле будут идемпотентами, причем
. Элементы е и/, указанные в определении, на самом деле будут идемпотентами, причем  Кроме того, в Б. п. каждое из условий
Кроме того, в Б. п. каждое из условий  ,
,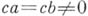 влечет
влечет  , а условия
, а условия  влекут
влекут 