"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
УНИФОРМИЗАЦИЯ
Значение УНИФОРМИЗАЦИЯ в математической энциклопедии:
множества  (или
(или  - тройка (f, D, G), где f=(f1, . . ., fN) - система мероморфных в области
- тройка (f, D, G), где f=(f1, . . ., fN) - система мероморфных в области  (соответственно
(соответственно 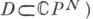 функций, определяющая голоморфное накрытие
функций, определяющая голоморфное накрытие  причем f(D0) плотно в A,a G - собственно разрывная группа биголоморфных автоморфизмов D, ограничение к-рой на D0 служит группой накрывающих гомеоморфизмов этого накрытия, т. е. D0/Gбиголоморфно эквивалентно f(D0).
причем f(D0) плотно в A,a G - собственно разрывная группа биголоморфных автоморфизмов D, ограничение к-рой на D0 служит группой накрывающих гомеоморфизмов этого накрытия, т. е. D0/Gбиголоморфно эквивалентно f(D0).
Можно говорить также об У. многозначных аналитических функций 
 понимая под этим У. множества A={(z, w)};это соответствует параметризации Fс помощью однозначных мероморфных функций.
понимая под этим У. множества A={(z, w)};это соответствует параметризации Fс помощью однозначных мероморфных функций.
Напр., комплексная кривая z2+w2=l в  униформизируется тройкой
униформизируется тройкой  где z=cos t, w=sin t, G - группа сдвигов
где z=cos t, w=sin t, G - группа сдвигов  или тройкой ((z, w), D, G), где
или тройкой ((z, w), D, G), где

G - тривиальная группа. Менее тривиальный пример дает кубическая кривая w2=a0z3+a1z2+a2z+a3, к-рая не допускает рациональной параметризации, но может быть униформизирована с помощью эллиптических функций, а именно тройкой ((f1, f2), D, G), где f1 и f2 - рациональные функции от  -функции Вейерштрасса
-функции Вейерштрасса  и ее производной с соответствующими периодами
и ее производной с соответствующими периодами  а G - группа, порожденная сдвигами
а G - группа, порожденная сдвигами 
Проблема У. произвольной алгебраич. кривой, определяемой общим алгебраич. уравнением

где Р- неприводимый алгебраич. многочлен над С, возникла еще в 1-й пол. 19 в., в частности в связи с интегрированием алгебраич. функций. А. Пуанкаре (Н. Poincare) поставил вопрос об У. множества решений произвольных аналитич. равнений вида (*), когда Р - сходящийся степенной ряд от двух переменных, рассматриваемый с его всевозможными аналитич. родолжениями. У. алгебраич. и произвольных аналитич. многообразий составляет содержание двадцать второй проблемы Гильберта. Полного решения проблемы У. тюка (к 1984) не получено, за исключением одномерного случая.
Введя во множестве пар (z, w) в  удовлетворяющих (*), комплексную структуру с помощью элементов соответствующей алгебраич. функции w(z) (или z(w)), получают компактную риманову поверхность, при этом координаты точек кривой (*) будут мероморфными функциями на этой поверхности. Более того, все компактные римановы поверхности с точностью до конформной эквивалентности получаются таким образом. Поэтому проблема У. алгебраич. кривых сводится к проблеме У. римановых поверхностен.
удовлетворяющих (*), комплексную структуру с помощью элементов соответствующей алгебраич. функции w(z) (или z(w)), получают компактную риманову поверхность, при этом координаты точек кривой (*) будут мероморфными функциями на этой поверхности. Более того, все компактные римановы поверхности с точностью до конформной эквивалентности получаются таким образом. Поэтому проблема У. алгебраич. кривых сводится к проблеме У. римановых поверхностен.
У. произвольной римановой поверхности Sназ. <тройка  где D - область на римановой сфере
где D - область на римановой сфере  - регулярное голоморфное накрытие с накрывающей группой Gконформных автоморфизмов D. Общая проблемa заключается в нахождении и описании всех возможных таких троек для данной римановой поверхности.
- регулярное голоморфное накрытие с накрывающей группой Gконформных автоморфизмов D. Общая проблемa заключается в нахождении и описании всех возможных таких троек для данной римановой поверхности.
Возможность У. любой римановой поверхности S, дающая принципиальное решение проблемы, была установлена в классич. работах П. Кебе (P. Koebe), А. Пуанкаре и Ф. Клейна (F. Klein); было получено окончательное решение, дающее описание всех возможных У. поверхности . (см. [4] - [6]). Справедлива теорема униформизации Клейна - Пуанкаре (доказанная в общем случае Л. Пуанкаре, см. [2]); каждая риманова поверхность Sконформно эквивалентна фактору D/G, где D- одна из трех канонических областей: риманова сфера  комплексная плоскость
комплексная плоскость  единичный круг
единичный круг  a G- собственно разрывная группа мёбиусовых (дробно-линейных) автоморфизмов D, определяемая с точностью до сопряжения в группе всех мёбиусовых автоморфизмов D.
a G- собственно разрывная группа мёбиусовых (дробно-линейных) автоморфизмов D, определяемая с точностью до сопряжения в группе всех мёбиусовых автоморфизмов D.
Случаи  и
и  взаимно исключают друг друга. Поверхности Sс такими универсальными голоморфными накрытиями наз. соответственно эллиптическими, параболическими и гиперболическими. При этом
взаимно исключают друг друга. Поверхности Sс такими универсальными голоморфными накрытиями наз. соответственно эллиптическими, параболическими и гиперболическими. При этом  только в случае, когда сама Sконформно эквивалентна
только в случае, когда сама Sконформно эквивалентна  (и, значит, G тривиальна);
(и, значит, G тривиальна);  когда S конформно эквивалентна либо
когда S конформно эквивалентна либо  либо
либо  либо тору, и соответственно этому Gлибо тривиальна, либо есть группа, порожденная сдвигом
либо тору, и соответственно этому Gлибо тривиальна, либо есть группа, порожденная сдвигом  либо есть группа, порожденная двумя сдвигами
либо есть группа, порожденная двумя сдвигами  где
где  - комплексные числа с
- комплексные числа с 
 В остальных случаях Sконформно эквивалентна
В остальных случаях Sконформно эквивалентна  где G- фуксова группа без кручения.
где G- фуксова группа без кручения.
Каноническая проекция  является неразветвленным накрытием и униформизирует все функции f на S, так как функции
является неразветвленным накрытием и униформизирует все функции f на S, так как функции  однозначны в D. Теорема Клейна - Пуанкаре обобщается и на разветвленные накрытия с заданными порядками ветвления.
однозначны в D. Теорема Клейна - Пуанкаре обобщается и на разветвленные накрытия с заданными порядками ветвления.
Несколько др. подход к проблеме У. (см. [3]) опирается на принцип: если риманова поверхность  гомео-морфна области
гомео-морфна области  (не обязательно односвязной), то
(не обязательно односвязной), то  и конформно эквивалентна D. Тем самым проблема У. сводится к топологич. проблеме нахождения всех (вообще говоря, разветвленных) плоских накрытий
и конформно эквивалентна D. Тем самым проблема У. сводится к топологич. проблеме нахождения всех (вообще говоря, разветвленных) плоских накрытий  данной римановой поверхности 5. Решение этих проблем дается следующими теоремами Маскита (см. [4], [5]).
данной римановой поверхности 5. Решение этих проблем дается следующими теоремами Маскита (см. [4], [5]).
I. Пусть S- ориентируемая поверхность, v1,. . ., vn,. . .- множество простых попарно не пересекающихся петель на S. Если  - регулярное накрытие с определяющей подгруппой
- регулярное накрытие с определяющей подгруппой  где
где  - натуральные числа, то
- натуральные числа, то  - плоская поверхность, т. е. гомеоморфна области в
- плоская поверхность, т. е. гомеоморфна области в 
II. Пусть  - плоская поверхность и
- плоская поверхность и  - регулярное накрытие ориентируемой поверхности Sс определяющей подгруппой N. Если S - поверхность конечного типа, т. е.
- регулярное накрытие ориентируемой поверхности Sс определяющей подгруппой N. Если S - поверхность конечного типа, т. е.  конечно порождена, то существуют конечное множество простых попарно не пересекающихся петель v1,. . ., vn и такие натуральные числа
конечно порождена, то существуют конечное множество простых попарно не пересекающихся петель v1,. . ., vn и такие натуральные числа  что
что 
III. Если  - плоская риманова поверхность и
- плоская риманова поверхность и  - собственно разрывная группа конформных автоморфизмов
- собственно разрывная группа конформных автоморфизмов  то существует конформный гомеоморфизм
то существует конформный гомеоморфизм  такой, что
такой, что  есть клейнова группа с инвариантной компонентой D.
есть клейнова группа с инвариантной компонентой D.
Таким образом, каждая риманова поверхность униформизируется клейновой группой. Напр., если S - замкнутая риманова поверхность рода  то ее фундаментальная группа имеет копредставление
то ее фундаментальная группа имеет копредставление

и в качестве определяющей плоское накрытие  нормальной подгруппы Nможно взять наименьшую нормальную подгруппу, порожденную al,. . ., ag (или b1,. . ., bg);тогда Sуниформизируется группой Шотки G рода g - свободной чисто локсодромической клейновой группой с gобразующими (классич. теорема Кёбе о разрезах).
нормальной подгруппы Nможно взять наименьшую нормальную подгруппу, порожденную al,. . ., ag (или b1,. . ., bg);тогда Sуниформизируется группой Шотки G рода g - свободной чисто локсодромической клейновой группой с gобразующими (классич. теорема Кёбе о разрезах).
У. римановых поверхностей конечного типа возможные клейновы группы могут быть классифицированы. Для этого используется понятие факторподгруппы. Если G - клейнова группа с инвариантной компонентой D(G), то ее подгруппа Нназ. факторнодгруппой G, если Н - максимальная подгруппа, для к-рой: а) ее инвариантная компонента  односвязна; b) Hне содержит случайных параболических элементов g(т. е. таких параболич. элементов, что при конформном изоморфизме
односвязна; b) Hне содержит случайных параболических элементов g(т. е. таких параболич. элементов, что при конформном изоморфизме 
 образ
образ  будет гиперболическим); с) каждый параболический элемент Gс неподвижной точкой на предельном множестве Нпринадлежит H. Напр., в теореме Клейна - Пуанкаре каждая факторподгруппа G совпадает с самой G, а в теореме Кебе о разрезах все факторподгрупиы G тривиальны. У.
будет гиперболическим); с) каждый параболический элемент Gс неподвижной точкой на предельном множестве Нпринадлежит H. Напр., в теореме Клейна - Пуанкаре каждая факторподгруппа G совпадает с самой G, а в теореме Кебе о разрезах все факторподгрупиы G тривиальны. У.  римановой поверхности S, где D- инвариантная компонента G, наз. стандартной, если G не имеет кручения и не содержит случайных параболич. элементов. Для замкнутых поверхностей все такие У. описываются следующей теоремой (см. [6]).
римановой поверхности S, где D- инвариантная компонента G, наз. стандартной, если G не имеет кручения и не содержит случайных параболич. элементов. Для замкнутых поверхностей все такие У. описываются следующей теоремой (см. [6]).
Пусть S- замкнутая риманова поверхность рода g>0 и {vl,. . ., vn} - множество простых попарно не пересекающихся петель на S. Тогда существует единственная с точностью до конформной эквивалентности стандартная У.  поверхности S такая, что каждая факторподгруппа G является либо фуксовой, либо элементарной и накрытие
поверхности S такая, что каждая факторподгруппа G является либо фуксовой, либо элементарной и накрытие  построено по наименьшей нормальной подгруппе
построено по наименьшей нормальной подгруппе  натянутой на петли v1, . . ., v п.
натянутой на петли v1, . . ., v п.
Теория квазиконформных отображений и Тайхмюллера пространств позволила доказать возможность одновременной У. нескольких римановых поверхностей одной клейновой группой, а также всех римановых поверхностей данного типа (см. [7]).
Лит.:[1] Klein Сhr. F., лMath. Ann.

 (или
(или  - тройка (f, D, G), где f=(f1, . . ., fN) - система мероморфных в области
- тройка (f, D, G), где f=(f1, . . ., fN) - система мероморфных в области  (соответственно
(соответственно 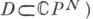 функций, определяющая голоморфное накрытие
функций, определяющая голоморфное накрытие  причем f(D0) плотно в A,a G - собственно разрывная группа биголоморфных автоморфизмов D, ограничение к-рой на D0 служит группой накрывающих гомеоморфизмов этого накрытия, т. е. D0/Gбиголоморфно эквивалентно f(D0).
причем f(D0) плотно в A,a G - собственно разрывная группа биголоморфных автоморфизмов D, ограничение к-рой на D0 служит группой накрывающих гомеоморфизмов этого накрытия, т. е. D0/Gбиголоморфно эквивалентно f(D0). 
 понимая под этим У. множества A={(z, w)};это соответствует параметризации Fс помощью однозначных мероморфных функций.
понимая под этим У. множества A={(z, w)};это соответствует параметризации Fс помощью однозначных мероморфных функций.  униформизируется тройкой
униформизируется тройкой  где z=cos t, w=sin t, G - группа сдвигов
где z=cos t, w=sin t, G - группа сдвигов  или тройкой ((z, w), D, G), где
или тройкой ((z, w), D, G), где 
 -функции Вейерштрасса
-функции Вейерштрасса  и ее производной с соответствующими периодами
и ее производной с соответствующими периодами  а G - группа, порожденная сдвигами
а G - группа, порожденная сдвигами 

 удовлетворяющих (*), комплексную структуру с помощью элементов соответствующей алгебраич. функции w(z) (или z(w)), получают компактную риманову поверхность, при этом координаты точек кривой (*) будут мероморфными функциями на этой поверхности. Более того, все компактные римановы поверхности с точностью до конформной эквивалентности получаются таким образом. Поэтому проблема У. алгебраич. кривых сводится к проблеме У. римановых поверхностен.
удовлетворяющих (*), комплексную структуру с помощью элементов соответствующей алгебраич. функции w(z) (или z(w)), получают компактную риманову поверхность, при этом координаты точек кривой (*) будут мероморфными функциями на этой поверхности. Более того, все компактные римановы поверхности с точностью до конформной эквивалентности получаются таким образом. Поэтому проблема У. алгебраич. кривых сводится к проблеме У. римановых поверхностен.  где D - область на римановой сфере
где D - область на римановой сфере  - регулярное голоморфное накрытие с накрывающей группой Gконформных автоморфизмов D. Общая проблемa заключается в нахождении и описании всех возможных таких троек для данной римановой поверхности.
- регулярное голоморфное накрытие с накрывающей группой Gконформных автоморфизмов D. Общая проблемa заключается в нахождении и описании всех возможных таких троек для данной римановой поверхности.  комплексная плоскость
комплексная плоскость  единичный круг
единичный круг  a G- собственно разрывная группа мёбиусовых (дробно-линейных) автоморфизмов D, определяемая с точностью до сопряжения в группе всех мёбиусовых автоморфизмов D.
a G- собственно разрывная группа мёбиусовых (дробно-линейных) автоморфизмов D, определяемая с точностью до сопряжения в группе всех мёбиусовых автоморфизмов D.  и
и  взаимно исключают друг друга. Поверхности Sс такими универсальными голоморфными накрытиями наз. соответственно эллиптическими, параболическими и гиперболическими. При этом
взаимно исключают друг друга. Поверхности Sс такими универсальными голоморфными накрытиями наз. соответственно эллиптическими, параболическими и гиперболическими. При этом  только в случае, когда сама Sконформно эквивалентна
только в случае, когда сама Sконформно эквивалентна  (и, значит, G тривиальна);
(и, значит, G тривиальна);  когда S конформно эквивалентна либо
когда S конформно эквивалентна либо  либо
либо  либо тору, и соответственно этому Gлибо тривиальна, либо есть группа, порожденная сдвигом
либо тору, и соответственно этому Gлибо тривиальна, либо есть группа, порожденная сдвигом  либо есть группа, порожденная двумя сдвигами
либо есть группа, порожденная двумя сдвигами  где
где  - комплексные числа с
- комплексные числа с 
 В остальных случаях Sконформно эквивалентна
В остальных случаях Sконформно эквивалентна  где G- фуксова группа без кручения.
где G- фуксова группа без кручения.  является неразветвленным накрытием и униформизирует все функции f на S, так как функции
является неразветвленным накрытием и униформизирует все функции f на S, так как функции  однозначны в D. Теорема Клейна - Пуанкаре обобщается и на разветвленные накрытия с заданными порядками ветвления.
однозначны в D. Теорема Клейна - Пуанкаре обобщается и на разветвленные накрытия с заданными порядками ветвления.  гомео-морфна области
гомео-морфна области  (не обязательно односвязной), то
(не обязательно односвязной), то  и конформно эквивалентна D. Тем самым проблема У. сводится к топологич. проблеме нахождения всех (вообще говоря, разветвленных) плоских накрытий
и конформно эквивалентна D. Тем самым проблема У. сводится к топологич. проблеме нахождения всех (вообще говоря, разветвленных) плоских накрытий  данной римановой поверхности 5. Решение этих проблем дается следующими теоремами Маскита (см. [4], [5]).
данной римановой поверхности 5. Решение этих проблем дается следующими теоремами Маскита (см. [4], [5]).  - регулярное накрытие с определяющей подгруппой
- регулярное накрытие с определяющей подгруппой  где
где  - натуральные числа, то
- натуральные числа, то  - плоская поверхность, т. е. гомеоморфна области в
- плоская поверхность, т. е. гомеоморфна области в 
 - плоская поверхность и
- плоская поверхность и  - регулярное накрытие ориентируемой поверхности Sс определяющей подгруппой N. Если S - поверхность конечного типа, т. е.
- регулярное накрытие ориентируемой поверхности Sс определяющей подгруппой N. Если S - поверхность конечного типа, т. е.  конечно порождена, то существуют конечное множество простых попарно не пересекающихся петель v1,. . ., vn и такие натуральные числа
конечно порождена, то существуют конечное множество простых попарно не пересекающихся петель v1,. . ., vn и такие натуральные числа  что
что 
 - плоская риманова поверхность и
- плоская риманова поверхность и  - собственно разрывная группа конформных автоморфизмов
- собственно разрывная группа конформных автоморфизмов  то существует конформный гомеоморфизм
то существует конформный гомеоморфизм  такой, что
такой, что  есть клейнова группа с инвариантной компонентой D.
есть клейнова группа с инвариантной компонентой D.  то ее фундаментальная группа имеет копредставление
то ее фундаментальная группа имеет копредставление 
 нормальной подгруппы Nможно взять наименьшую нормальную подгруппу, порожденную al,. . ., ag (или b1,. . ., bg);тогда Sуниформизируется группой Шотки G рода g - свободной чисто локсодромической клейновой группой с gобразующими (классич. теорема Кёбе о разрезах).
нормальной подгруппы Nможно взять наименьшую нормальную подгруппу, порожденную al,. . ., ag (или b1,. . ., bg);тогда Sуниформизируется группой Шотки G рода g - свободной чисто локсодромической клейновой группой с gобразующими (классич. теорема Кёбе о разрезах).  односвязна; b) Hне содержит случайных параболических элементов g(т. е. таких параболич. элементов, что при конформном изоморфизме
односвязна; b) Hне содержит случайных параболических элементов g(т. е. таких параболич. элементов, что при конформном изоморфизме 
 образ
образ  будет гиперболическим); с) каждый параболический элемент Gс неподвижной точкой на предельном множестве Нпринадлежит H. Напр., в теореме Клейна - Пуанкаре каждая факторподгруппа G совпадает с самой G, а в теореме Кебе о разрезах все факторподгрупиы G тривиальны. У.
будет гиперболическим); с) каждый параболический элемент Gс неподвижной точкой на предельном множестве Нпринадлежит H. Напр., в теореме Клейна - Пуанкаре каждая факторподгруппа G совпадает с самой G, а в теореме Кебе о разрезах все факторподгрупиы G тривиальны. У.  римановой поверхности S, где D- инвариантная компонента G, наз. стандартной, если G не имеет кручения и не содержит случайных параболич. элементов. Для замкнутых поверхностей все такие У. описываются следующей теоремой (см. [6]).
римановой поверхности S, где D- инвариантная компонента G, наз. стандартной, если G не имеет кручения и не содержит случайных параболич. элементов. Для замкнутых поверхностей все такие У. описываются следующей теоремой (см. [6]).  поверхности S такая, что каждая факторподгруппа G является либо фуксовой, либо элементарной и накрытие
поверхности S такая, что каждая факторподгруппа G является либо фуксовой, либо элементарной и накрытие  построено по наименьшей нормальной подгруппе
построено по наименьшей нормальной подгруппе  натянутой на петли v1, . . ., v п.
натянутой на петли v1, . . ., v п.