|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БОТТА ТЕОРЕМА ПЕРИОДИЧНОСТИЗначение БОТТА ТЕОРЕМА ПЕРИОДИЧНОСТИ в математической энциклопедии: основная теорема К-теории, в простейшем виде утверждающая, что для любого (компактного) пространства Xсуществует изоморфизм между кольцами Б. т. п. устанавливает аакономерность свойства стабильного гомотопич. типа унитарной группы Лит.:[1] Воtt R., "Ann. math.", 1959, v. 70, p. 313-37; [2] Милнор Д ж., Теория Морса, пер. с англ., М., 1965; [3] Атья м., Лекция по К-теории, пер. с англ., М., 1967; [4] Xьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970; [5] Мооrе I. С., On the periodicity theorem for complex vector bundles, Seminaire H. Cartan, 1959-60; [6] Atiуah M., Bott R., "Acta math.", 1964, v. 112, p. 229-47. А. Ф. Щекутьев. БOXHEPA ИНТЕГРАЛ - интеграл от функции со значениями в банаховом пространстве по скалярной мере. Б. и. принадлежит к так наз. сильным интегралам. Пусть Функция
Функция Для такой функции интегралом Бохнера по множеству где Критерий интегрируемости по Бохнеру: для того чтобы сильно измеримая функция Множество функций, интегрируемых по Бохнеру, образует векторное подпространство Свойства Б. и.: 1) 2) Б. и. есть счетно аддитивная и абсолютно непрерывная функция множеств б) при 3) если и 4) пространство 5) если T-замкнутый линейный оператор из банахова пространства хв банахово пространство уи то в случае ограниченности Тусловие выполняется автоматически ([3] -[5]). Б. <и. введен С. Бохнером [1]. Эквивалентные определения даны Т. Гильденбрандтом [2] и Н. Данфордом (интеграл D0). Лит.:[1] Bochner S., "Fundam. math.", 1933, t. 20, p. 262- 76; 12] Hi1debrandt Т., "Bull. Amer. Math. Soc.", 1953, v. 59; p. 1ll-39; [3] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [4] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., [2 изд.], М., 1962; [5] Данфорд Н., Шварц Д ж. Т., Линейные операторы, пер. с англ., т. 1 - Общая теория, Ы., 1962. В. И. Соболев. |
|
|
|

 и
и  . Более общо, если L - линейное комплексное расслоение над
. Более общо, если L - линейное комплексное расслоение над  - проективизация расслоения
- проективизация расслоения  , то кольцо
, то кольцо  представляет собой
представляет собой  -алгебру с одной образующей [Н]и единственным соотношением
-алгебру с одной образующей [Н]и единственным соотношением  здесь
здесь  - образ расслоения Ев кольце
- образ расслоения Ев кольце  ,
,  -расслоение Хопфа над
-расслоение Хопфа над  . Этот факт равносилен существованию изоморфизма Тома в K-теории для комплексных векторных расслоений. В частности,
. Этот факт равносилен существованию изоморфизма Тома в K-теории для комплексных векторных расслоений. В частности, Б. -т. п. впервые доказана P. Боттом [1] с использованием теории Морса и получила переформулировку в терминах K-теории [6]; также доказано утверждение, аналогичное Б. т. п., для вещественных расслоений.
Б. -т. п. впервые доказана P. Боттом [1] с использованием теории Морса и получила переформулировку в терминах K-теории [6]; также доказано утверждение, аналогичное Б. т. п., для вещественных расслоений. , состоящую в том, что
, состоящую в том, что  - пространство петель на X,~ -слабая гомотопич. эквивалентность, в частности
- пространство петель на X,~ -слабая гомотопич. эквивалентность, в частности  для i=0, 1, . . ., pi ,есть i-я гомотопич. группа; аналогично, для ортогональной группы О п:
для i=0, 1, . . ., pi ,есть i-я гомотопич. группа; аналогично, для ортогональной группы О п:
 - векторное пространство функций
- векторное пространство функций  со значениями и банаховом пространстве X, заданных на пространстве
со значениями и банаховом пространстве X, заданных на пространстве  со счетно аддитивной скалярной мерой
со счетно аддитивной скалярной мерой  на
на  -алгебре
-алгебре  подмножеств множества Е. Функция
подмножеств множества Е. Функция  наз. простой, если
наз. простой, если 
 наз. сил к но измеримой, если существует последовательность
наз. сил к но измеримой, если существует последовательность  простых функций и
простых функций и  почти всюду относительно меры
почти всюду относительно меры  на
на  . В этом случае скалярная функция
. В этом случае скалярная функция 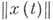 является
является  -измеримой. Для простой функции
-измеримой. Для простой функции 

 наз. интегрируемой по Бохнеру, если она сильно измерима и если для любой аппроксимирующей последовательности
наз. интегрируемой по Бохнеру, если она сильно измерима и если для любой аппроксимирующей последовательности  простых функций
простых функций 
 наз.
наз.
 - характеристич. функция множества В, а предел понимается в смысле сильной сходимости в банаховом пространстве X. Этот предел существует и не зависит от выбора аппроксимирующей последовательности простых функций.
- характеристич. функция множества В, а предел понимается в смысле сильной сходимости в банаховом пространстве X. Этот предел существует и не зависит от выбора аппроксимирующей последовательности простых функций. была интегрируема по Бохнеру, необходимо и достаточно, чтобы норма этой функции была интегрируема, т. е.
была интегрируема по Бохнеру, необходимо и достаточно, чтобы норма этой функции была интегрируема, т. е.
 пространства F, а Б. и. есть аддитивный и однородный оператор на этом подпространстве.
пространства F, а Б. и. есть аддитивный и однородный оператор на этом подпространстве.
 -алгебры
-алгебры  , т. е.
, т. е.
 равномерно по
равномерно по  ;
;
 почти всюду относительно меры
почти всюду относительно меры  на
на  и
и  почти всюду относительно
почти всюду относительно  на В, причем ,
на В, причем ,

 полно относительно сходимости по норме:
полно относительно сходимости по норме:


