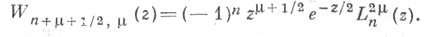" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

УИТТЕКЕРА ФУНКЦИИ

Значение УИТТЕКЕРА ФУНКЦИИ в математической энциклопедии:

- функции и 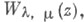к-рые являются решениями дифференциального Уиттекера уравнения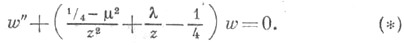

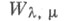Функция вводится равенством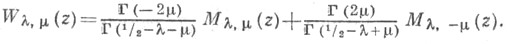

Пары функций 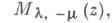и и 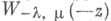- линейно независимые решения уравнения (*). Точка z=0 - точка ветвления для 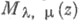и 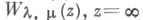- существенно особая точка.
Связь с другими функциями: С вырожденной гипергеометрической функцией:

с модифицированной Бесселя функцией и Макдональда функцией:

с интегралом вероятности:

с Лагерра многочленами:

Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., [2 изд.], т. 2, М., 1974; [2] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963.
Ю. А. Брычков, А. П. Прудников.