|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БОРЕЛЯ - КАНТЕЛЛИ ЛЕММАЗначение БОРЕЛЯ - КАНТЕЛЛИ ЛЕММА в математической энциклопедии: - одно из часто используемых утверждений о бесконечных последовательностях случайных событий. Пусть
справедливо равенство Если события Лит.:[1] Воrеl Е., "Rend. Circolo mat. Palermo", 1909, v. 27, p. 247-71; [2] Сante11i P. P., "Atti Accad. naz. Lincei", 1917, v. 26; [3] Лоэв М., Теория вероятностей, пер. с англ., М., 1962, с. 242-43. А. В. Прохоров. |
|
|
|
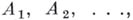
- последовательность нек-рых событий и А - событие, состоящее в наступлении конечного числа из событий 
Б.- К. л. утверждает, что при условии
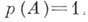
взаимно независимы, то 
или 0 в зависимости от того, сходится или расходится ряд 
т. е. в этом случае для 
условие (*) является необходимым и достаточным (так наз. критерий Бореля "нуль или единица", см. Нуль-единица закон). Известны распространения последнего критерия на нек-рые классы зависимых событий. В.- К. л. используется, напр., при доказательстве больших чисел усиленного закона.