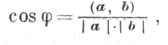УГОЛ

Значение УГОЛ в математической энциклопедии:

- геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало - вершиной У. Пусть [ ВА),[ ВС) - стороны угла, В - его вершина, - плоскость, определяемая сторонами У. Фигура делит плоскость на две фигуры Фигура i==l, 2, также наз. У. или плоским углом, наз. внутренней областью плоского У.
Два угла наз. равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины. От любого луча на плоскости в данную сторону от него можно отложить единственный У., равный данному У. Сравнение У. осуществляется двумя способами. Если У. рассматривается как пара лучей с общим началом, то для выяснения вопроса, какой из двух У. больше, необходимо совместить в одной плоскости вершины У. и одну пару их сторон (см. рис. 1). Если вторая сторона одного У. окажется расположенной внутри другого У., то говорят, что первый У. меньше, чем второй. Второй способ сравнения У. основан на сопоставлении каждому У. нек-рого числа. Равным У. будет соответствовать одинаковое число градусов или радиан (см. ниже), большему У.- большее число, меньшему -меньшее.

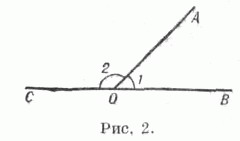
Два У. наз. смежными, если у них общая вершина и одна сторона, а две другие стороны образуют прямую (см. рис. 2). Вообще, У., имеющие общую вершину и одну общую сторону, наз. прилежащими. У. наз. вертикальными, если стороны одного являются продолжениями за вершину сторон другого У. Вертикальные У. равны между собой. У., у к-рого стороны образуют прямую, наз. развернутым. Половина развернутого У. наз. прямым У. Прямой У. можно эквивалентно определить иначе: У., равный своему смежному, наз. прямым. Внутренняя область плоского У., не превосходящего развернутого, является выпуклой областью на плоскости. За единицу измерения У. принимается 90-я доля прямого У., наз. градусом.

Используется и т. <н. круговая, или радианная, мера У. Числовое значение радианной меры У. равно длине дуги, высекаемой сторонами У. из единичной окружности. Один радиан приписывается У., соответствующему дуге, длина к-рой равна ее радиусу. Развернутый У. равен радиан.
При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются У. (см. рис. 3): 1 и 5, 2 и 6, 4 и 8, З и 7 - наз. соответственными; 2 и 5, 3 и 8 - внутренними односторонними; 1 и 6, 4 и 7 - внешними односторонними; 3 и 5, 2 и 8- внутренними накрест лежащими; 1 и 7, 4 и 6 - внешними накрест лежащими.

В практич. задачах целесообразно рассматривать У. как меру поворота фиксированного луча вокруг его начала до заданного положения. В зависимости от направления поворота У. в этом случае можно рассматривать как положительные, так и отрицательные. Тем самым У. в этом смысле может иметь своей величиной любое действительное число. У. как мера поворота луча рассматривается в теории тригонометрич. функций: для любых значений аргумента (У.) можно определить значения тригонометрич. функций. Понятие У. в геометрич. системе, в основу к-рой положена точечно-векторная аксиоматика, в корне отличается от определений У. как фигуры - в этой аксиоматике под У. понимают определенную метрич. величину, связанную с двумя векторами с помощью операции скалярного умножения векторов. Именно, каждая пара векторов аи bопределяет нек-рый угол - число, связанное с векторами формулой

где (a, b) - скалярное произведение векторов.
Понятие У. как плоской фигуры и как нек-рой числовой величины применяется в различных геометрич. задачах, в к-рых У. определяется специальным образом. Так, под У. между пересекающимися кривыми, имеющими определенные касательные в точке пересечения, понимают У., образованный этими касательными.
За угол между прямой и плоскостью принимается У., образованный прямой и ее прямоугольной проекцией на плоскость; он измеряется в пределах от 0