"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТУЭ МЕТОДЗначение ТУЭ МЕТОД в математической энциклопедии:
- метод в теории диофантовых приближений, созданный А. Туэ [1] в связи с проблемой приближения алгебраич. чисел рациональными числами: найти величину v=v(n), при к-рой для каждого алгебраич. числа  степени n неравенство степени n неравенство  (1) (1)
имеет коночное число решений в целых рациональных числах ри q, q>0,при любом 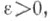 и бесконечное число решений при любом и бесконечное число решений при любом 
А. Туэ показал, что  Т. м. основан на свойствах специального многочлена j(x, у )от двух переменных х, у с целыми коэффициентами и предположении существования двух решений неравенства (1) при Т. м. основан на свойствах специального многочлена j(x, у )от двух переменных х, у с целыми коэффициентами и предположении существования двух решений неравенства (1) при  с достаточно большими значениями q. Теорема Туэ имеет много важных приложений в теории чисел. В частности, из нее следует, что диофантово уравнение с достаточно большими значениями q. Теорема Туэ имеет много важных приложений в теории чисел. В частности, из нее следует, что диофантово уравнение 
где F(x, у)- неприводимая форма от переменныx хи у с целыми коэффициентами степени  а т - целое число, может иметь не более, чем конечное число, решений в целых числах хи у. а т - целое число, может иметь не более, чем конечное число, решений в целых числах хи у.
Окончательную оценку величины v в неравенстве (1) получил К. Рог (К. Roth, [2]) путем обобщения Т. м. на случай многочлена любого числа переменных, подобного многочлену f(x, у), и использования большего числа решений неравенства (1). Результат - теорема Туэ - 3игеля - Рота: v=2 для любого  Т. м. имеет обобщение на случай приближения алгебраич. чисел алгебраич. числами. Т. м. является общим методом доказательства конечности целых точек на широкого класса кривых алгебраич. многообразий (см. Диофантова геометрия, Диофантово множество). Наряду с этим Т. м. имеет существенный недостаток - является неэффективным методом в том смысле, что не дает ответа на вопрос, существуют ли на самом деле используемые в доказательствах решения неравенств (1) или соответствующих уравнений (2). Таким образом, Т. м., решая вопрос о конечности числа решений уравнения (2), не дает возможности определить, разрешимо ли конкретное уравнение такого типа и каковы количествен, оценки решений х, у в зависимости от F. Т. м. имеет обобщение на случай приближения алгебраич. чисел алгебраич. числами. Т. м. является общим методом доказательства конечности целых точек на широкого класса кривых алгебраич. многообразий (см. Диофантова геометрия, Диофантово множество). Наряду с этим Т. м. имеет существенный недостаток - является неэффективным методом в том смысле, что не дает ответа на вопрос, существуют ли на самом деле используемые в доказательствах решения неравенств (1) или соответствующих уравнений (2). Таким образом, Т. м., решая вопрос о конечности числа решений уравнения (2), не дает возможности определить, разрешимо ли конкретное уравнение такого типа и каковы количествен, оценки решений х, у в зависимости от F.
См. также Диофантовых приближений проблемы эффективизации.
Лит.:[1] Тhue A. лJ. reme angew. Math.
|

 степени n неравенство
степени n неравенство  (1)
(1) 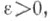 и бесконечное число решений при любом
и бесконечное число решений при любом 
 Т. м. основан на свойствах специального многочлена j(x, у )от двух переменных х, у с целыми коэффициентами и предположении существования двух решений неравенства (1) при
Т. м. основан на свойствах специального многочлена j(x, у )от двух переменных х, у с целыми коэффициентами и предположении существования двух решений неравенства (1) при  с достаточно большими значениями q. Теорема Туэ имеет много важных приложений в теории чисел. В частности, из нее следует, что диофантово уравнение
с достаточно большими значениями q. Теорема Туэ имеет много важных приложений в теории чисел. В частности, из нее следует, что диофантово уравнение 
 а т - целое число, может иметь не более, чем конечное число, решений в целых числах хи у.
а т - целое число, может иметь не более, чем конечное число, решений в целых числах хи у.  Т. м. имеет обобщение на случай приближения алгебраич. чисел алгебраич. числами. Т. м. является общим методом доказательства конечности целых точек на широкого класса кривых алгебраич. многообразий (см. Диофантова геометрия, Диофантово множество). Наряду с этим Т. м. имеет существенный недостаток - является неэффективным методом в том смысле, что не дает ответа на вопрос, существуют ли на самом деле используемые в доказательствах решения неравенств (1) или соответствующих уравнений (2). Таким образом, Т. м., решая вопрос о конечности числа решений уравнения (2), не дает возможности определить, разрешимо ли конкретное уравнение такого типа и каковы количествен, оценки решений х, у в зависимости от F.
Т. м. имеет обобщение на случай приближения алгебраич. чисел алгебраич. числами. Т. м. является общим методом доказательства конечности целых точек на широкого класса кривых алгебраич. многообразий (см. Диофантова геометрия, Диофантово множество). Наряду с этим Т. м. имеет существенный недостаток - является неэффективным методом в том смысле, что не дает ответа на вопрос, существуют ли на самом деле используемые в доказательствах решения неравенств (1) или соответствующих уравнений (2). Таким образом, Т. м., решая вопрос о конечности числа решений уравнения (2), не дает возможности определить, разрешимо ли конкретное уравнение такого типа и каковы количествен, оценки решений х, у в зависимости от F.