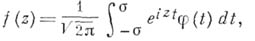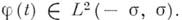|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БОРЕЛЯ ПРЕОБРАЗОВАНИЕЗначение БОРЕЛЯ ПРЕОБРАЗОВАНИЕ в математической энциклопедии: интегральное преобразование вида где то ряд сходится при Пусть - опорная функция множества При дополнительных условиях из этой формулы могут быть выведены и другие представления. Так, пусть имеется класс целых функций Этот класс совпадает с классом функций где
Лит.:[1] Воrе1 Е., Lemons sur les series divergentes, 2 ed., P., 1928; [2] Джpбашян M. M.. Интегральные преобразования и представления функций в комплексной области, М., 1966. А. Ф. Леонтьев. |
|
|
|


 - целая функция экспоненциального типа. Б. п. есть частный случай Лапласа преобразования. Функция
- целая функция экспоненциального типа. Б. п. есть частный случай Лапласа преобразования. Функция  наз. ассоциированной функцией (по Борелю) с f(z). Если
наз. ассоциированной функцией (по Борелю) с f(z). Если 

 , где
, где  - тип функции
- тип функции  .
. - наименьшее выпуклое замкнутое множество, содержащее все особенности функции
- наименьшее выпуклое замкнутое множество, содержащее все особенности функции  ,
,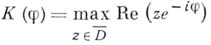
 и
и  - индикатриса роста функции
- индикатриса роста функции  . Тогда
. Тогда  Если интегрирование в Б. п. происходит по лучу
Если интегрирование в Б. п. происходит по лучу  то соответствующий интеграл сходится в полуплоскости
то соответствующий интеграл сходится в полуплоскости  Пусть С - замкнутый контур, охватывающий D. Тогда
Пусть С - замкнутый контур, охватывающий D. Тогда 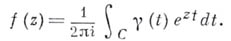
 экспоненциального типа
экспоненциального типа  , для к-рых
, для к-рых 
 , допускающих представление
, допускающих представление