"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТРАНСФИНИТНЫЙ ДИАМЕТР
Значение ТРАНСФИНИТНЫЙ ДИАМЕТР в математической энциклопедии:
компактного множества - характеристика d=d(E)компактного множества Ена комплексной плоскости, служащая геометрии, интерпретацией емкости этого множества. Пусть Е- компактное бесконечное множество плоскости z. Величина

где [ а, b]=|а-b| - евклидово расстояние между точками а, b, наз. п- мдиаметром множества Е. В частности, d2 (Е)- евклидов диаметр множества Е. Точки zn,1. . . ., zn,n множества Е, для к-рых в правой части равенства (1) реализуется максимум, наз. точками Фекете (или узлами Вандермонда) для Е. Последовательность величин dn(E)невозрастающая:  п=2, 3, . . ., так что существует предел
п=2, 3, . . ., так что существует предел

Величина d(E)и наз. трансфинитным диаметром множества Е. Если Е- конечное множество, то полагают d(E)=0.Т. д. d(E), Чебышева постоянная 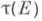 и емкость множества С(Е)связаны равенствами
и емкость множества С(Е)связаны равенствами 
Т. д. множества Еобладает следующими свойствами: 1) если  то
то  2) если а- фиксированное комплексное число и
2) если а- фиксированное комплексное число и  то d(E1)=|a|d(E);3) если
то d(E1)=|a|d(E);3) если  - множество точек, находящихся на расстоянии от Е, меньшем или равном e, то
- множество точек, находящихся на расстоянии от Е, меньшем или равном e, то  4) если Е* - множество всех корней уравнения
4) если Е* - множество всех корней уравнения

где Q(z) - данный многочлен, . пробегает множество Е, то  Т. д. круга равен его радиусу; Т. <д. прямолинейного отрезка равен четверти его длины.
Т. д. круга равен его радиусу; Т. <д. прямолинейного отрезка равен четверти его длины.
Пусть Е- ограниченный континуум, D - та из компонент дополнения Едо расширенной плоскости, к-рая содержит точку  Тогда Т. д. Еравен конформному радиусу области D(относительно точки
Тогда Т. д. Еравен конформному радиусу области D(относительно точки 
Соответствующие понятия для множеств на гиперболич. и эллиптич. плоскостях определяются следующим образом. Пусть в качестве модели гиперболич. плоскости рассматривается круг |z| <1 с метрикой, определяемой линейным элементом  и пусть Е- замкнутое бесконечное множество в круге |z|<l. Тогда n-й гиперболический диаметр dn,h(E)множества . определяется равенством (1), в к-ром
и пусть Е- замкнутое бесконечное множество в круге |z|<l. Тогда n-й гиперболический диаметр dn,h(E)множества . определяется равенством (1), в к-ром

- гиперболическое псевдорасстояние между точками а и b, т. е.  где
где  - гиперболич. расстояние между точками а, b круга |z|<l (см. Гиперболическая метрика). Как и в евклидовом случае, последовательность dn,h(E) невозрастающая, и существует предел
- гиперболич. расстояние между точками а, b круга |z|<l (см. Гиперболическая метрика). Как и в евклидовом случае, последовательность dn,h(E) невозрастающая, и существует предел

наз. гиперболическим трансфинитным диаметром множества Е. Определяя гиперболическую постоянную Чебышева  и гиперболическую емкость С h (Е)множества Епосредством гиперболич. псевдорасстояния (2) между точками круга |z|<l аналогично тому, как постоянная Чебышева
и гиперболическую емкость С h (Е)множества Епосредством гиперболич. псевдорасстояния (2) между точками круга |z|<l аналогично тому, как постоянная Чебышева  и емкость С(Е)
и емкость С(Е)
определяются при помощи евклидова расстояния между точками плоскости z, получают равенства

Гиперболич. Т. д. инвариантен относительно полной группы гиперболич. изометрий. Если Е - континуум, то имеется простая связь гиперболич. Т. д. dh(E)сконформным отображением. Именно, пусть Е - континуум в круге |z| <1 и дополнение . до круга |z|<1 конформно эквивалентно круговому кольцу r<|w|<1, 0<r<1. Тогда r=dh(E).
Пусть в качестве модели эллиптич. плоскости взята расширенная плоскость zс метрикой ее римановой сферы . диаметра 1, касающейся плоскости zв точке z=0, т. e. метрикой, определяемой линейным элементом dse=|dz|/(1 + |z|2). при этом пусть отождествлены точки z и z*=-1/z, к-рым при стереографич. проекции расширенной плоскости z на сферу . соответствуют диаметрально противоположные точки на К. Пусть Е - замкнутое бесконечное множество на расширенной плоскости z,  где
где  Тогда n-й эллиптический диаметр dn,е (Е)множества . определяется равенством (1), в к-рoм
Тогда n-й эллиптический диаметр dn,е (Е)множества . определяется равенством (1), в к-рoм

- эллиптическое псевдорасстояние между точками а, b множества Е, т. е, где
где  - эллиптич. расстояние между аи b, Как и в предыдущих случаях, последовательность dn,e(E)невозрастающая, и существует предел
- эллиптич. расстояние между аи b, Как и в предыдущих случаях, последовательность dn,e(E)невозрастающая, и существует предел  называемый эллиптическим трансфинитным диаметром множества Е. Определяя эллиптическую постоянную Чебышева
называемый эллиптическим трансфинитным диаметром множества Е. Определяя эллиптическую постоянную Чебышева  иэллиптическую емкость С е (Е)множества Епосредством эллиптич. псевдорасстояния (3), получают равенства:
иэллиптическую емкость С е (Е)множества Епосредством эллиптич. псевдорасстояния (3), получают равенства:

Эллиптич. Т. д. de(E) инвариантен относительно группы дробно-линейных преобразований

расширенной плоскости . на себя, дополненной группой отражений относительно эллиптич. прямых. Первая из этих групп изоморфна группе вращений сферы Котносительно ее центра, вторая - группе отражений сферы Котносительно плоскостей, проходящих через ее центр. При данном определении эллиптич. Т. д. множества Еследующим образом связан с конформным отображением. Если Е - континуум на расширенной плоскости z,  и дополнение
и дополнение  до расширенной плоскости конформно эквивалентно круговому кольцу r<|w|<l/r, 0<r<1, то r=de(E).
до расширенной плоскости конформно эквивалентно круговому кольцу r<|w|<l/r, 0<r<1, то r=de(E).
Понятие Т. д. допускает обобщение для компактов Ев многомерном евклидовом пространстве  связанное с потенциала теорией. Пусть для точек
связанное с потенциала теорией. Пусть для точек 

- фундаментальное решение уравнения Лапласа, и для набора точек  пусть
пусть

Тогда при т=2 справедливо равенство

а при  целесообразно принять (см. [4])
целесообразно принять (см. [4])

Лит.:[1] Fеkсte M.,лMath. Z.


 п=2, 3, . . ., так что существует предел
п=2, 3, . . ., так что существует предел 
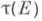 и емкость множества С(Е)связаны равенствами
и емкость множества С(Е)связаны равенствами 
 то
то  2) если а- фиксированное комплексное число и
2) если а- фиксированное комплексное число и  то d(E1)=|a|d(E);3) если
то d(E1)=|a|d(E);3) если  - множество точек, находящихся на расстоянии от Е, меньшем или равном e, то
- множество точек, находящихся на расстоянии от Е, меньшем или равном e, то  4) если Е* - множество всех корней уравнения
4) если Е* - множество всех корней уравнения 
 Т. д. круга равен его радиусу; Т. <д. прямолинейного отрезка равен четверти его длины.
Т. д. круга равен его радиусу; Т. <д. прямолинейного отрезка равен четверти его длины.  Тогда Т. д. Еравен конформному радиусу области D(относительно точки
Тогда Т. д. Еравен конформному радиусу области D(относительно точки 
 и пусть Е- замкнутое бесконечное множество в круге |z|<l. Тогда n-й гиперболический диаметр dn,h(E)множества . определяется равенством (1), в к-ром
и пусть Е- замкнутое бесконечное множество в круге |z|<l. Тогда n-й гиперболический диаметр dn,h(E)множества . определяется равенством (1), в к-ром 
 где
где  - гиперболич. расстояние между точками а, b круга |z|<l (см. Гиперболическая метрика). Как и в евклидовом случае, последовательность dn,h(E) невозрастающая, и существует предел
- гиперболич. расстояние между точками а, b круга |z|<l (см. Гиперболическая метрика). Как и в евклидовом случае, последовательность dn,h(E) невозрастающая, и существует предел 
 и гиперболическую емкость С h (Е)множества Епосредством гиперболич. псевдорасстояния (2) между точками круга |z|<l аналогично тому, как постоянная Чебышева
и гиперболическую емкость С h (Е)множества Епосредством гиперболич. псевдорасстояния (2) между точками круга |z|<l аналогично тому, как постоянная Чебышева  и емкость С(Е)
и емкость С(Е) 
 где
где  Тогда n-й эллиптический диаметр dn,е (Е)множества . определяется равенством (1), в к-рoм
Тогда n-й эллиптический диаметр dn,е (Е)множества . определяется равенством (1), в к-рoм 
 где
где  - эллиптич. расстояние между аи b, Как и в предыдущих случаях, последовательность dn,e(E)невозрастающая, и существует предел
- эллиптич. расстояние между аи b, Как и в предыдущих случаях, последовательность dn,e(E)невозрастающая, и существует предел  называемый эллиптическим трансфинитным диаметром множества Е. Определяя эллиптическую постоянную Чебышева
называемый эллиптическим трансфинитным диаметром множества Е. Определяя эллиптическую постоянную Чебышева  иэллиптическую емкость С е (Е)множества Епосредством эллиптич. псевдорасстояния (3), получают равенства:
иэллиптическую емкость С е (Е)множества Епосредством эллиптич. псевдорасстояния (3), получают равенства: 

 и дополнение
и дополнение  до расширенной плоскости конформно эквивалентно круговому кольцу r<|w|<l/r, 0<r<1, то r=de(E).
до расширенной плоскости конформно эквивалентно круговому кольцу r<|w|<l/r, 0<r<1, то r=de(E).  связанное с потенциала теорией. Пусть для точек
связанное с потенциала теорией. Пусть для точек 

 пусть
пусть 

 целесообразно принять (см. [4])
целесообразно принять (см. [4]) 