"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БОРЕЛЯ МЕРА
Значение БОРЕЛЯ МЕРА в математической энциклопедии:
множеств- неотрицательная функция m подмножеств топологич. пространства X, обладающая следующими свойствами: 1) область ее определения есть  -алгебра
-алгебра  борелевских множеств из X, т. е. наименьший класс подмножеств из X, содержащий открытые множества и замкнутый относительно теоретико-множественных операций, производимых в счетном числе; 2)
борелевских множеств из X, т. е. наименьший класс подмножеств из X, содержащий открытые множества и замкнутый относительно теоретико-множественных операций, производимых в счетном числе; 2) при
при  то есть
то есть  счетно аддитивна. Б. м.
счетно аддитивна. Б. м. наз. регулярной, если
наз. регулярной, если

где  принадлежит классу
принадлежит классу  замкнутых подмножеств из X. Нередко изучение Б. м. связывают с изучением мер Бэра, к-рые отличаются от Б. м. лишь областью их определения: они определены на наименьшей
замкнутых подмножеств из X. Нередко изучение Б. м. связывают с изучением мер Бэра, к-рые отличаются от Б. м. лишь областью их определения: они определены на наименьшей  -алгебре
-алгебре  , относительно к-рой измеримы все непрерывные функции на X. Б. м.
, относительно к-рой измеримы все непрерывные функции на X. Б. м. (соответственно мера Бэра
(соответственно мера Бэра  ) наз.
) наз. -гладкой, если
-гладкой, если  для любой сети
для любой сети  замкнутых множеств, удовлетворяющей условию
замкнутых множеств, удовлетворяющей условию 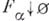 (соответственно
(соответственно  для любой сети
для любой сети  множеств, являющихся нулями непрерывных функций, при условии, что
множеств, являющихся нулями непрерывных функций, при условии, что  Б. м.
Б. м.  (соответственно мера Бэра v) наз. п л о тн о и, если
(соответственно мера Бэра v) наз. п л о тн о и, если 
 , где
, где  -класс компактных подмножеств из
-класс компактных подмножеств из  X(соответственно
X(соответственно 

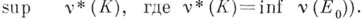
 Плотность и
Плотность и  -гладкость являются ограничениями, обеспечивающими дополнительную гладкость мер, и часто выполняются в конкретных .ситуациях. При определенных условиях меры Бэра могут быть продолжены до Б. м. Напр., если Xвполне регулярно и хаусдорфово, то всякая
-гладкость являются ограничениями, обеспечивающими дополнительную гладкость мер, и часто выполняются в конкретных .ситуациях. При определенных условиях меры Бэра могут быть продолжены до Б. м. Напр., если Xвполне регулярно и хаусдорфово, то всякая  -гладкая (плотная) конечная мера Бэра может быть продолжена до регулярной
-гладкая (плотная) конечная мера Бэра может быть продолжена до регулярной  -гладкой (плотной) конечной Б. м. При изучении мер на локально компактных пространствах Б. м. (соответственно мерами Бэра) наз. иногда меры, определенные на
-гладкой (плотной) конечной Б. м. При изучении мер на локально компактных пространствах Б. м. (соответственно мерами Бэра) наз. иногда меры, определенные на  -кольце множеств, порожденном компактными (соответственно компактными
-кольце множеств, порожденном компактными (соответственно компактными  ) множествами, и конечные на компактных множествах. Мерой Бореля на прямой часто наз. меру, определенную на борелевских множествах и такую, что ее значение на произвольном отрезке равно длине этого отрезка.
) множествами, и конечные на компактных множествах. Мерой Бореля на прямой часто наз. меру, определенную на борелевских множествах и такую, что ее значение на произвольном отрезке равно длине этого отрезка.
Лит.: [1] Варадарайн В. С., "Матем. сб.", 1961, т. 55, № 1, с. 35-100; [2] Xалмош П., Теория меры, пер. с англ., М., 1953; [3] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969. В. В. Сазонов.

 -алгебра
-алгебра  борелевских множеств из X, т. е. наименьший класс подмножеств из X, содержащий открытые множества и замкнутый относительно теоретико-множественных операций, производимых в счетном числе; 2)
борелевских множеств из X, т. е. наименьший класс подмножеств из X, содержащий открытые множества и замкнутый относительно теоретико-множественных операций, производимых в счетном числе; 2) при
при  то есть
то есть  счетно аддитивна. Б. м.
счетно аддитивна. Б. м. наз. регулярной, если
наз. регулярной, если 
 принадлежит классу
принадлежит классу  замкнутых подмножеств из X. Нередко изучение Б. м. связывают с изучением мер Бэра, к-рые отличаются от Б. м. лишь областью их определения: они определены на наименьшей
замкнутых подмножеств из X. Нередко изучение Б. м. связывают с изучением мер Бэра, к-рые отличаются от Б. м. лишь областью их определения: они определены на наименьшей  -алгебре
-алгебре  , относительно к-рой измеримы все непрерывные функции на X. Б. м.
, относительно к-рой измеримы все непрерывные функции на X. Б. м. (соответственно мера Бэра
(соответственно мера Бэра  ) наз.
) наз. -гладкой, если
-гладкой, если  для любой сети
для любой сети  замкнутых множеств, удовлетворяющей условию
замкнутых множеств, удовлетворяющей условию 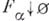 (соответственно
(соответственно  для любой сети
для любой сети  множеств, являющихся нулями непрерывных функций, при условии, что
множеств, являющихся нулями непрерывных функций, при условии, что  Б. м.
Б. м.  (соответственно мера Бэра v) наз. п л о тн о и, если
(соответственно мера Бэра v) наз. п л о тн о и, если 
 , где
, где  -класс компактных подмножеств из
-класс компактных подмножеств из  X(соответственно
X(соответственно 

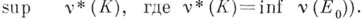
 Плотность и
Плотность и  -гладкость являются ограничениями, обеспечивающими дополнительную гладкость мер, и часто выполняются в конкретных .ситуациях. При определенных условиях меры Бэра могут быть продолжены до Б. м. Напр., если Xвполне регулярно и хаусдорфово, то всякая
-гладкость являются ограничениями, обеспечивающими дополнительную гладкость мер, и часто выполняются в конкретных .ситуациях. При определенных условиях меры Бэра могут быть продолжены до Б. м. Напр., если Xвполне регулярно и хаусдорфово, то всякая  -гладкая (плотная) конечная мера Бэра может быть продолжена до регулярной
-гладкая (плотная) конечная мера Бэра может быть продолжена до регулярной  -гладкой (плотной) конечной Б. м. При изучении мер на локально компактных пространствах Б. м. (соответственно мерами Бэра) наз. иногда меры, определенные на
-гладкой (плотной) конечной Б. м. При изучении мер на локально компактных пространствах Б. м. (соответственно мерами Бэра) наз. иногда меры, определенные на  -кольце множеств, порожденном компактными (соответственно компактными
-кольце множеств, порожденном компактными (соответственно компактными  ) множествами, и конечные на компактных множествах. Мерой Бореля на прямой часто наз. меру, определенную на борелевских множествах и такую, что ее значение на произвольном отрезке равно длине этого отрезка.
) множествами, и конечные на компактных множествах. Мерой Бореля на прямой часто наз. меру, определенную на борелевских множествах и такую, что ее значение на произвольном отрезке равно длине этого отрезка.