"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТРАНСФИНИТНАЯ ИНДУКЦИЯЗначение ТРАНСФИНИТНАЯ ИНДУКЦИЯ в математической энциклопедии:
принцип, позволяющий утверждать суждение (х)для любого элемента хвполне упорядоченного класса Е, если установлено, что для всякого 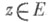 из истинности (у)для всех y<z следует истинность A(z): из истинности (у)для всех y<z следует истинность A(z): 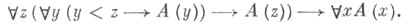
Когда Е- отрезок ординалов, меньших 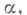 эквивалентна такая формулировка: если эквивалентна такая формулировка: если 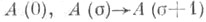 и и  сохраняется при предельном переходе сохраняется при предельном переходе 
то  для любого для любого 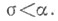 Частным случаем Т. и. является математическая индукция. Если отношение < на классе Езадает фундированное дерево (т. е. дерево, все ветви к-рого обрываются), то Т. и. для такого Еэквивалентна бар-индукции: из того, что Аверно для всех концевых вершин и наследуется при движении от них к корню, следует, что Аверно для корня. Эта форма важна в интуиционистской математике. Доказуемостью Т. и. до различных ординалов измеряют дедуктивную силу формальных систем. Частным случаем Т. и. является математическая индукция. Если отношение < на классе Езадает фундированное дерево (т. е. дерево, все ветви к-рого обрываются), то Т. и. для такого Еэквивалентна бар-индукции: из того, что Аверно для всех концевых вершин и наследуется при движении от них к корню, следует, что Аверно для корня. Эта форма важна в интуиционистской математике. Доказуемостью Т. и. до различных ординалов измеряют дедуктивную силу формальных систем. Г. Е. Минц.
|

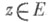 из истинности (у)для всех y<z следует истинность A(z):
из истинности (у)для всех y<z следует истинность A(z): 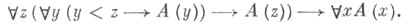
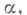 эквивалентна такая формулировка: если
эквивалентна такая формулировка: если 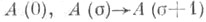 и
и  сохраняется при предельном переходе
сохраняется при предельном переходе 
 для любого
для любого 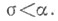 Частным случаем Т. и. является математическая индукция. Если отношение < на классе Езадает фундированное дерево (т. е. дерево, все ветви к-рого обрываются), то Т. и. для такого Еэквивалентна бар-индукции: из того, что Аверно для всех концевых вершин и наследуется при движении от них к корню, следует, что Аверно для корня. Эта форма важна в интуиционистской математике. Доказуемостью Т. и. до различных ординалов измеряют дедуктивную силу формальных систем.
Частным случаем Т. и. является математическая индукция. Если отношение < на классе Езадает фундированное дерево (т. е. дерево, все ветви к-рого обрываются), то Т. и. для такого Еэквивалентна бар-индукции: из того, что Аверно для всех концевых вершин и наследуется при движении от них к корню, следует, что Аверно для корня. Эта форма важна в интуиционистской математике. Доказуемостью Т. и. до различных ординалов измеряют дедуктивную силу формальных систем.