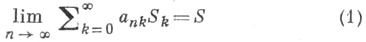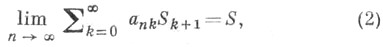|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТРАНСЛЯТИВНОСТЬ МЕТОДА СУММИРОВАНИЯЗначение ТРАНСЛЯТИВНОСТЬ МЕТОДА СУММИРОВАНИЯ в математической энциклопедии: свойство метода, сохраняющее суммируемость ряда после добавления к нему или удаления из него конечного числа членов. Более точно: метод суммирования Аназ. транслятивным, если из суммируемости ряда
всегда следует
и наоборот. В случаях, когда такое заключение выполняется только в одну сторону, метод называют транслятивным справа - если из (1) следует (2), но обратное неверно, или транслятивным слева, когда из (2) следует (1), но обратное неверно. Лит.:[1] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960; [2] Барон С., Введение в теорию суммируемости рядов, 2 изд., Таллин, 1977. |
|
|
|

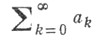
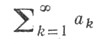
 то это означает, что из
то это означает, что из