|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОРОИДАЛЬНАЯ ГАРМОНИКАЗначение ТОРОИДАЛЬНАЯ ГАРМОНИКА в математической энциклопедии: - функция точки на торе, появляющаяся при решении уравнения Лапласа методом разделения переменных в тороидальных координатах
где
Лит.:[1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 5 изд., М., 1977; [2] Морс Ф. М., Фешбах Г., Методы теоретической физики, пер. с англ., т. 1 - 2, М., 1960. |
|
|
|

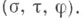 Гармонич. функция
Гармонич. функция  являющаяся решением уравнения Лапласа, записывается в виде ряда
являющаяся решением уравнения Лапласа, записывается в виде ряда 
 - присоединенные функции Лежандра с полуцелым индексом. Полагая здесь
- присоединенные функции Лежандра с полуцелым индексом. Полагая здесь  получают Т. г., или, иначе, поверхностную Т. г., в отличие от членов ряда (*), зависящих от трёх переменных
получают Т. г., или, иначе, поверхностную Т. г., в отличие от членов ряда (*), зависящих от трёх переменных  , к-рые иногда наз. пространственными Т. г.
, к-рые иногда наз. пространственными Т. г. 
 - функции Лежандра 2-го рода:
- функции Лежандра 2-го рода: