|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОПОСЗначение ТОПОС в математической энциклопедии: - категория, эквивалентная категории пучков множеств на нек-рой топологизиронанной категории. Другое определение: Т.- это такая категория С, что любой пучок в канонич. топологии на Спредставим. Для объектов Т. (являющихся пучками множеств) определены обычные конструкции в категории множеств. По этой причине Т. могут служить нестандартными моделями теории множеств. При этом удобнее пользоваться более общим определением: элементарный топос - это категория Сс произведениями и финальным объектом 1, контравариантным функтором Лит.:Theоriеdes topos et cohomologle etale des schemas, t. 1-3, B. - [e. a.], 1972-73; [2] Cohomologie etale, В.- [с. a.], 1977; [3] Саrtier Р., в кн.: Seminaire Bourbaki, v. 1977/ 1978, В.- [e. a.], 1979. |
|
|
|
(при этом 
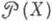для 
понимается как множество частей X)и мономорфизмами 
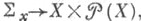где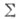 
- график отношения принадлежности. Множество 
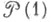служит естественной областью значений логич. высказываний в топосе С.