"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОПОЛОГИЧЕСКОЕ ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ
Значение ТОПОЛОГИЧЕСКОЕ ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ в математической энциклопедии:
локально выпуклых пространств E1 и Е 2 - локально выпуклое пространство, обладающее свойством универсальности по отношению к заданным на  билинейным операторам с нек-рым условием непрерывности. Точнее, пусть
билинейным операторам с нек-рым условием непрерывности. Точнее, пусть  - нек-рый класс локально выпуклых пространств и для каждого
- нек-рый класс локально выпуклых пространств и для каждого  задано подмножество Т(F)множества рездельно непрерывных билинейных операторов из
задано подмножество Т(F)множества рездельно непрерывных билинейных операторов из  в F. Тогда Т. т. п. E1 и Е 2 (относительно класса Т(F))наз. локально выпуклое пространство
в F. Тогда Т. т. п. E1 и Е 2 (относительно класса Т(F))наз. локально выпуклое пространство  вместе с оператором
вместе с оператором  обладающее следующим свойством: для любого
обладающее следующим свойством: для любого  существует единственный непрерывный линейный оператор
существует единственный непрерывный линейный оператор  такой, что
такой, что  Таким образом, если ситуация позволяет говорить о функторе
Таким образом, если ситуация позволяет говорить о функторе 
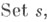 то
то  определено как представляющий объект этого функтора.
определено как представляющий объект этого функтора.
Во всех известных (1985) примерах  содержит поле комплексных чисел
содержит поле комплексных чисел  а
а  содержит все билинейные функционалы вида
содержит все билинейные функционалы вида  переводящие ( х, у )в i(x) g(y). В этом случае, если Т. т. п. существует, то в
переводящие ( х, у )в i(x) g(y). В этом случае, если Т. т. п. существует, то в  есть плотное подпространство, к-рое можно отождествить с пространством
есть плотное подпространство, к-рое можно отождествить с пространством  алгебраического тензорного произведения;при этом
алгебраического тензорного произведения;при этом 
Если  состоит из всех раздельно (соответственно, совместно) непрерывных билинейных операторов, то Т. т. п. наз. индуктивным (соответственно, проективным). Наиболее важно проективное Т. т. п. Пусть { р i} - определяющие семейства полунорм в Е i, i=l, 2; через p обозначается топология в
состоит из всех раздельно (соответственно, совместно) непрерывных билинейных операторов, то Т. т. п. наз. индуктивным (соответственно, проективным). Наиболее важно проективное Т. т. п. Пусть { р i} - определяющие семейства полунорм в Е i, i=l, 2; через p обозначается топология в  определенная семейством полунорм
определенная семейством полунорм

Тогда если  - класс всех, соответственно, всех полных локально выпуклых пространств, то проективное Т. т. п. E1 и Е 2 существует и его локально выпуклое пространство есть
- класс всех, соответственно, всех полных локально выпуклых пространств, то проективное Т. т. п. E1 и Е 2 существует и его локально выпуклое пространство есть  с топологией
с топологией  соответственно, его пополнение.
соответственно, его пополнение.
Если Ei - банаховы пространства с нормами р i, i=l, 2, то  - норма в
- норма в  пополнение но к-рой обозначается через
пополнение но к-рой обозначается через  Элементы
Элементы  имеютдля каждого
имеютдля каждого  представление
представление

где

Если снабдить  более слабой, чем
более слабой, чем  топологией с помощью семейства полунорм
топологией с помощью семейства полунорм 

где Vи W - поляры единичных шаров относительно р1 и р 2, то возникает Т. т. п., иногда наз. слабым. Локально выпуклые пространства E1,обладающие тем свойством, что для любого Е 2 обе топологии в  совпадают, образуют важный класс ядерных пространств.
совпадают, образуют важный класс ядерных пространств.
Проективное Т. т. п. связано с понятием свойства аппроксимации: локально выпуклое пространство Е 1 обладает свойством аппроксимации, если для каждого предкомпактного множества  и окрестности нуля Uсуществует непрерывный оператор конечного ранга
и окрестности нуля Uсуществует непрерывный оператор конечного ранга  такой, что для всех
такой, что для всех 
 Все ядерные пространства обладают свойством аппроксимации. Банахово пространство Е 1 обладает свойством аппроксимации тогда и только тогда, когда для любого банахова пространства Е 2 оператор
Все ядерные пространства обладают свойством аппроксимации. Банахово пространство Е 1 обладает свойством аппроксимации тогда и только тогда, когда для любого банахова пространства Е 2 оператор  однозначно определенный равенством
однозначно определенный равенством  имеет нулевое ядро. Построено [3] сепарабельное банахово пространство без свойства аппроксимации (и тем самым доказано существование банаховых пространств без базиса Шаудера, поскольку последние всегда имеют свойство аппроксимации,- т. о. отрицательно решена т. н. лпроблема базиса
имеет нулевое ядро. Построено [3] сепарабельное банахово пространство без свойства аппроксимации (и тем самым доказано существование банаховых пространств без базиса Шаудера, поскольку последние всегда имеют свойство аппроксимации,- т. о. отрицательно решена т. н. лпроблема базиса

 билинейным операторам с нек-рым условием непрерывности. Точнее, пусть
билинейным операторам с нек-рым условием непрерывности. Точнее, пусть  - нек-рый класс локально выпуклых пространств и для каждого
- нек-рый класс локально выпуклых пространств и для каждого  задано подмножество Т(F)множества рездельно непрерывных билинейных операторов из
задано подмножество Т(F)множества рездельно непрерывных билинейных операторов из  в F. Тогда Т. т. п. E1 и Е 2 (относительно класса Т(F))наз. локально выпуклое пространство
в F. Тогда Т. т. п. E1 и Е 2 (относительно класса Т(F))наз. локально выпуклое пространство  вместе с оператором
вместе с оператором  обладающее следующим свойством: для любого
обладающее следующим свойством: для любого  существует единственный непрерывный линейный оператор
существует единственный непрерывный линейный оператор  такой, что
такой, что  Таким образом, если ситуация позволяет говорить о функторе
Таким образом, если ситуация позволяет говорить о функторе 
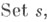 то
то  определено как представляющий объект этого функтора.
определено как представляющий объект этого функтора.  содержит поле комплексных чисел
содержит поле комплексных чисел  а
а  содержит все билинейные функционалы вида
содержит все билинейные функционалы вида  переводящие ( х, у )в i(x) g(y). В этом случае, если Т. т. п. существует, то в
переводящие ( х, у )в i(x) g(y). В этом случае, если Т. т. п. существует, то в  есть плотное подпространство, к-рое можно отождествить с пространством
есть плотное подпространство, к-рое можно отождествить с пространством  алгебраического тензорного произведения;при этом
алгебраического тензорного произведения;при этом 
 состоит из всех раздельно (соответственно, совместно) непрерывных билинейных операторов, то Т. т. п. наз. индуктивным (соответственно, проективным). Наиболее важно проективное Т. т. п. Пусть { р i} - определяющие семейства полунорм в Е i, i=l, 2; через p обозначается топология в
состоит из всех раздельно (соответственно, совместно) непрерывных билинейных операторов, то Т. т. п. наз. индуктивным (соответственно, проективным). Наиболее важно проективное Т. т. п. Пусть { р i} - определяющие семейства полунорм в Е i, i=l, 2; через p обозначается топология в  определенная семейством полунорм
определенная семейством полунорм 
 - класс всех, соответственно, всех полных локально выпуклых пространств, то проективное Т. т. п. E1 и Е 2 существует и его локально выпуклое пространство есть
- класс всех, соответственно, всех полных локально выпуклых пространств, то проективное Т. т. п. E1 и Е 2 существует и его локально выпуклое пространство есть  с топологией
с топологией  соответственно, его пополнение.
соответственно, его пополнение.  - норма в
- норма в  пополнение но к-рой обозначается через
пополнение но к-рой обозначается через  Элементы
Элементы  имеютдля каждого
имеютдля каждого  представление
представление 

 более слабой, чем
более слабой, чем  топологией с помощью семейства полунорм
топологией с помощью семейства полунорм 

 совпадают, образуют важный класс ядерных пространств.
совпадают, образуют важный класс ядерных пространств.  и окрестности нуля Uсуществует непрерывный оператор конечного ранга
и окрестности нуля Uсуществует непрерывный оператор конечного ранга  такой, что для всех
такой, что для всех 
 Все ядерные пространства обладают свойством аппроксимации. Банахово пространство Е 1 обладает свойством аппроксимации тогда и только тогда, когда для любого банахова пространства Е 2 оператор
Все ядерные пространства обладают свойством аппроксимации. Банахово пространство Е 1 обладает свойством аппроксимации тогда и только тогда, когда для любого банахова пространства Е 2 оператор  однозначно определенный равенством
однозначно определенный равенством  имеет нулевое ядро. Построено [3] сепарабельное банахово пространство без свойства аппроксимации (и тем самым доказано существование банаховых пространств без базиса Шаудера, поскольку последние всегда имеют свойство аппроксимации,- т. о. отрицательно решена т. н. лпроблема базиса
имеет нулевое ядро. Построено [3] сепарабельное банахово пространство без свойства аппроксимации (и тем самым доказано существование банаховых пространств без базиса Шаудера, поскольку последние всегда имеют свойство аппроксимации,- т. о. отрицательно решена т. н. лпроблема базиса