"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО
Значение ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии:
совокупность двух объектов: множества X, состоящего из элементов произвольной природы, наз. точками данного пространства, и из введенной в это множество топологической структуры, или топологии, все равно - открытой или замкнутой (одна переходит в другую, если заменить множества, составляющие данную топологию, их дополнениями). Если не сказано противное, под топологией  будет пониматься открытая топология. Логически самый простой способ определения топологии в данном множестве Xзаключается в непосредственном указании тех подмножеств множества X, к-рые составляют эту топологию. Но часто проще определять не все множества, являющиеся элементами данной топологии, а только нек-рые множества этих элементов (т. е. базу данной топологии), достаточные для того, чтобы все остальные элементы топологии получались как объединения (в случае открытой топологии) или пересечения (в случае замкнутой) множеств, к-рые составляют базу. Так, напр., обычная топология числовой прямой получается, если определить в качестве базы ее открытой топологии множество всех интервалов (можно ограничиться даже одними интервалами с рациональными концами). Остальные открытые множества суть объединения интервалов.
будет пониматься открытая топология. Логически самый простой способ определения топологии в данном множестве Xзаключается в непосредственном указании тех подмножеств множества X, к-рые составляют эту топологию. Но часто проще определять не все множества, являющиеся элементами данной топологии, а только нек-рые множества этих элементов (т. е. базу данной топологии), достаточные для того, чтобы все остальные элементы топологии получались как объединения (в случае открытой топологии) или пересечения (в случае замкнутой) множеств, к-рые составляют базу. Так, напр., обычная топология числовой прямой получается, если определить в качестве базы ее открытой топологии множество всех интервалов (можно ограничиться даже одними интервалами с рациональными концами). Остальные открытые множества суть объединения интервалов.
Имея в виду базу открытой и, соответственно, замкнутой топологии, часто говорят об открытой, соответственно, замкнутой базе данного Т, п., причем открытые базы рассматриваются чаще замкнутых, поэтому если говорят просто о базе Т. п., то всегда имеют в виду его открытую базу. Наименьшее кардинальное число (в нетривиальных случаях бесконечное), являющееся мощностью какой-либо базы данного Т. п., наз. его весом. После мощности множества всех точек пространства вес является важнейшим т. н. кардинальнозначным инвариантом пространства. Особенно важны пространства, имеющие счетную базу; напр., числовая прямая есть такое пространство. Аналогично, счетная база евклидова га-мерного пространства получается, если взять т. н. рациональные (открытые) шары, т. е. шары, радиус к-рых и координаты центра к-рых суть рациональные числа. Часто приходится определять тем или иным стандартным (естественным) способом топологию во множестве, снабженном какой-либо другой структурой. Так, говорят об естественной топологии метрич. пространства или об естественной (интервальной) топологии упорядоченного множества. Первая имеет своей базой множество всех открытых шаров данного метрич. пространства, вторая - открытые интервалы данного линейно упорядоченного множества. Т. п. наз. метризуемым, если во множестве Xего точек можно ввести метрику  порождающую топологию данного Т. п. Метризуемые пространства образуют один из важнейших классов Т. п., и к центральным проблемам общей топологии принадлежали в течение нескольких десятилетий общая и специальная проблемы метризации, т. е. проблемы нахождения необходимых и достаточных условий для того, чтобы Т. п. или Т. п. того или иного специального класса было метризуемым. Эти условия составляют содержание общих или специальных метризационных теорем.
порождающую топологию данного Т. п. Метризуемые пространства образуют один из важнейших классов Т. п., и к центральным проблемам общей топологии принадлежали в течение нескольких десятилетий общая и специальная проблемы метризации, т. е. проблемы нахождения необходимых и достаточных условий для того, чтобы Т. п. или Т. п. того или иного специального класса было метризуемым. Эти условия составляют содержание общих или специальных метризационных теорем.
Всякое подмножество Х 0 множестра Xвсех точек данного Т. п. X,  естественно превращается в Т. п. (подпространство пространства
естественно превращается в Т. п. (подпространство пространства  с топологией, элементы к-рой суть всевозможные множества вида
с топологией, элементы к-рой суть всевозможные множества вида  где Г - любой элемент топологии
где Г - любой элемент топологии  Пусть дана (открытая) топология
Пусть дана (открытая) топология  в множестве X, превращающая это множество в Т. п.. X,
в множестве X, превращающая это множество в Т. п.. X, Т. к. топология есть множество нек-рых подмножеств множества X, то между различными топологиями в одном и том же множестве Xестественно устанавливается отношение (частичного) порядка (по включению), т. е. топология
Т. к. топология есть множество нек-рых подмножеств множества X, то между различными топологиями в одном и том же множестве Xестественно устанавливается отношение (частичного) порядка (по включению), т. е. топология  больше (или равна) топологии
больше (или равна) топологии  если
если  есть подмножество множества
есть подмножество множества  т. е. каждое множество, открытое в топологии
т. е. каждое множество, открытое в топологии  будет открытым и в топологии
будет открытым и в топологии  Если в пределах данного рассуждения речь идет об одной и той же топологии в данном множестве X, то обыкновенно Т. п. X,
Если в пределах данного рассуждения речь идет об одной и той же топологии в данном множестве X, то обыкновенно Т. п. X,  обозначается просто X. Из понятия топологии выводятся и все остальные основные топологич. понятия. Прежде всего замкнутые множества определяются как дополнения к открытым. Далее, окрестностью точки хв данном пространстве . наз. всякое открытое множество, содержащее точку х. Понятие окрестности позволяет сразу же определить и понятие точки прикосновения для любого множества
обозначается просто X. Из понятия топологии выводятся и все остальные основные топологич. понятия. Прежде всего замкнутые множества определяются как дополнения к открытым. Далее, окрестностью точки хв данном пространстве . наз. всякое открытое множество, содержащее точку х. Понятие окрестности позволяет сразу же определить и понятие точки прикосновения для любого множества  как такой точки, любая окрестность к-рой имеет непустое пересечение с множеством М. Из этого определения следует, что любая точка самого множества Мявляется точкой прикосновения этого множества. Множество всех точек прикосновения множества Мназ. замыканием множества Ми обозначается [М].Переход от любого множества Мк его замыканию наз. операцией замыкания в данном Т. п. Свойства этой операции: 1)
как такой точки, любая окрестность к-рой имеет непустое пересечение с множеством М. Из этого определения следует, что любая точка самого множества Мявляется точкой прикосновения этого множества. Множество всех точек прикосновения множества Мназ. замыканием множества Ми обозначается [М].Переход от любого множества Мк его замыканию наз. операцией замыкания в данном Т. п. Свойства этой операции: 1)  причем М=[М]тогда и только тогда, когда Мзамкнуто, т. е. его дополнение открыто;
причем М=[М]тогда и только тогда, когда Мзамкнуто, т. е. его дополнение открыто;
2)  3)
3)  Замыкание любого множества есть пересечение всех замкнутых множеств, содержащих множество М;другими словами, [М]есть наименьшее замкнутое множество, содержащее множество М.
Замыкание любого множества есть пересечение всех замкнутых множеств, содержащих множество М;другими словами, [М]есть наименьшее замкнутое множество, содержащее множество М.
Операция замыкания и ее основные свойства 1), 2),
3) получены, исходя из основного (в нашем изложении) понятия топологии или топологич. структуры, введенной в данное множество X. Можно было бы, наоборот, считать основным топологич. понятием понятие замыкания, т. е. считать, что в абстрактно данном множестве Xдля каждого подмножества Мопределено подмножество [М], наз. замыканием множества, так что выполнены свойства 1), 2), 3) (наз. в этом случае аксиомами замыкания, или аксиомами Куратовского) и 4)  На основе так введенного понятия замыкания замкнутые множества определятся как множества, совпадающие со своими замыканиями, а открытые множества - как множества, дополнительные к замкнутым; таким образом получается в точности топология в нашем первоначальном смысле, а операция замыкания, к к-рой она приводит, совпадает с той, к-рая была дана априори. Именно этот путь и был избран К. Куратовским (К. Кuratowski, 1922) для построения понятия Т. п. В 1925 II. С. Александровым были введены открытые топологич. структуры. Оба подхода приводят к одному и тому же классу Т. п., в настоящее время являющемуся общепринятым.
На основе так введенного понятия замыкания замкнутые множества определятся как множества, совпадающие со своими замыканиями, а открытые множества - как множества, дополнительные к замкнутым; таким образом получается в точности топология в нашем первоначальном смысле, а операция замыкания, к к-рой она приводит, совпадает с той, к-рая была дана априори. Именно этот путь и был избран К. Куратовским (К. Кuratowski, 1922) для построения понятия Т. п. В 1925 II. С. Александровым были введены открытые топологич. структуры. Оба подхода приводят к одному и тому же классу Т. п., в настоящее время являющемуся общепринятым.
С понятием Т. п. тесно связано понятие непрерывного отображения одного пространства в другое. Отображение  Т. п. Xв Т. п. Yнепрерывно в точке
Т. п. Xв Т. п. Yнепрерывно в точке  если для любой окрестности О у точки
если для любой окрестности О у точки  в пространстве Yсуществует такая окрестность О х точки хв X, что
в пространстве Yсуществует такая окрестность О х точки хв X, что  (условие Коши). При этом, не изменяя содержания определения, можно брать окрестности О у и О х из любых открытых баз соответственно пространств Yи X. В частности, для метрич. пространств это определение непрерывности переходит в обычное известное из курсов математич. анализа определение. Если отображение
(условие Коши). При этом, не изменяя содержания определения, можно брать окрестности О у и О х из любых открытых баз соответственно пространств Yи X. В частности, для метрич. пространств это определение непрерывности переходит в обычное известное из курсов математич. анализа определение. Если отображение  непрерывно в каждой точке
непрерывно в каждой точке  то оно наз. непрерывным отображением пространства X в пространство Y. Для непрерывности отображения
то оно наз. непрерывным отображением пространства X в пространство Y. Для непрерывности отображения  каждое из следующих условий необходимо и достаточно. 1) Если хесть точка прикосновения какого-либо множества
каждое из следующих условий необходимо и достаточно. 1) Если хесть точка прикосновения какого-либо множества  то f(x)есть точка прикосновения множества f(M)в F. 2) Полный прообраз f-1 (Г) всякого открытого в У множества Г есть открытое множество в X. Аналогично для замкнутых множеств.
то f(x)есть точка прикосновения множества f(M)в F. 2) Полный прообраз f-1 (Г) всякого открытого в У множества Г есть открытое множество в X. Аналогично для замкнутых множеств.
Если дано (непрерывное) отображение f Т. п. Xв Т. п. Y и Х а есть подпространство пространства X, то в силу отображения f пространство Х 0 отображается в Y и это отображение (наз. ограничением отображения  на подпространство Х 0) также непрерывно.
на подпространство Х 0) также непрерывно.
Важный частный случай непрерывных отображений образуют т. <п. факторные отображения, характеризующиеся каждым из следующих эквивалентных между собой условий. Множество  открыто (замкнуто) в У тогда и только тогда, когда f-1(B) обладает тем же свойством в X. Если непрерывное отображение f пространства Xна пространство У взаимно однозначно, то определено и обратное отображение
открыто (замкнуто) в У тогда и только тогда, когда f-1(B) обладает тем же свойством в X. Если непрерывное отображение f пространства Xна пространство У взаимно однозначно, то определено и обратное отображение  но это отображение может не быть непрерывным. Если же оно непрерывно, то каждое из отображений f, f-1 взаимно однозначно отображает топологию одного из пространств X, Y на топологию другого пространства. Тогда каждое из двух взаимно однозначных отображений f и f-l наз. топологическим отображением, или гомеомоpфизмом. Два пространства X и Y, из к-рых одно может быть гомеоморфно отображено на другое, наз. гомеоморфными или топологически эквивалентными между собою.
но это отображение может не быть непрерывным. Если же оно непрерывно, то каждое из отображений f, f-1 взаимно однозначно отображает топологию одного из пространств X, Y на топологию другого пространства. Тогда каждое из двух взаимно однозначных отображений f и f-l наз. топологическим отображением, или гомеомоpфизмом. Два пространства X и Y, из к-рых одно может быть гомеоморфно отображено на другое, наз. гомеоморфными или топологически эквивалентными между собою.
Непрерывное отображение  наз. неприводимым, если при этом отображении никакое отличное от всего Xзамкнутое множество Мне отображается на все Y.
наз. неприводимым, если при этом отображении никакое отличное от всего Xзамкнутое множество Мне отображается на все Y.
Конкретное изучение Т. п. связано прежде всего с выделением из общего класса этих пространств подклассов, характеризующихся теми или иными дополнительными условиями или аксиомами, кроме первоначальных аксиом, определяющих топологию пространства. Эти дополнительные аксиомы бывают разной природы. Прежде всего это группа т. н. аксиом отделимости. Первой аксиомой отделимости была аксиома Хаусдорфа, заключающаяся в требовании, чтобы любые две различные точки пространства были отделимы посредством окрестностей, т. е. содержались в дизъюнктных открытых множествах (совокупность двух или более множеств дизъюнктна или состоит из дизъюнктных множеств, если эти множества попарно не имеют общих элементов). Аксиома отделимости Хаусдорфа иначе наз. аксиомой Т 2,а удовлетворяющие ей Т. п. наз. хаусдорфовыми или Т 2 -пространствами. Определив эти пространства, Ф. Хаусдорф (F. Hausdorff) в 1914 впервые открыл достаточно широкий и в то же время достаточно богатый свойствами класс Т. п. и тем удовлетворил уже вполне назревшую к тому времени потребность математики. Дальнейшее развитие общей топологии исходит именно из хаусдорфовых пространств. Ослаблением аксиомы Т 2 является аксиомa T1,требующая, чтобы каждая из любых двух точек Т. п. имела окрестность, не содержащую вторую точку. Это требование равносильно требованию замкнутости в данном пространстве всякого множества, состоящего из конечного числа точек. Пространства, удовлетворяющие этому требованию; наз. T1 -пространствами. Еще более широкий класс Т. п. образуют T0 -пространства, т. е. пространства, в к-рых выполнена аксиома Т 0 (аксиома Колмогорова): из любых двух точек этого пространства по крайней мере одна имеет окрестность, не содержащую другую точку. T0 -пространства могут состоять из конечного числа и даже из двух точек, если одна точка образует замкнутое множество, но не открытое, а другая, наоборот, образует открытое, но не замкнутое множество (связное двоеточие).
Аксиома T3 требует, чтобы произвольная точка пространства и произвольное, не содержащее эту точку замкнутое множество были отделимы окрестностями, т. е. содержались соответственно в двух дизъюнктных открытых множествах. Пространства, удовлетворяющие аксиоме Т 3,наз. Т 3 -пространствами. Т 3 -пространство может не удовлетворять аксиоме T1, таково, напр., связное двоеточие. T0 -пространства, удовлетворяющие аксиоме T1, наз. регулярными; все они - хаусдорфовы пространства. Т. п. наз. Т 4 -пространством, если в нем всякие два дизъюнктные замкнутые множества имеют дизъюнктные окрестности. Т 4 -пространства, являющиеся в то же время T1 -пространствами, наз. нормальными, все они регулярны и подавно хаусдорфовы. Всякое множество Х 0 точек Т. п. X,  получает топологию, однозначно определенную топологией
получает топологию, однозначно определенную топологией  и таким образом становится топологич. подпространством пространства X,
и таким образом становится топологич. подпространством пространства X, При этом всякое подпространство пространства, удовлетворяющего аксиоме Ti, i=0, 1, 2, 3, также удовлетворяет аксиоме Т i, т. е. аксиомы Ti наследуются всеми подпространствами данного пространства. Аксиома Т 4 этим свойством не обладает: существуют нормальные пространства X, не все (даже открытые в X)подпространства к-рых нормальны. Однако если Х 0 -замкнутое множество в нормальном пространстве X, то подпространство Х 0 нормально.
При этом всякое подпространство пространства, удовлетворяющего аксиоме Ti, i=0, 1, 2, 3, также удовлетворяет аксиоме Т i, т. е. аксиомы Ti наследуются всеми подпространствами данного пространства. Аксиома Т 4 этим свойством не обладает: существуют нормальные пространства X, не все (даже открытые в X)подпространства к-рых нормальны. Однако если Х 0 -замкнутое множество в нормальном пространстве X, то подпространство Х 0 нормально.
До сих пор отделимость точек и множеств понималась в смысле наличия у них дизъюнктных окрестностей. Однако в современной топологии имеет значение и т. н. функциональная отделимость, впервые введенная П. С. Урысоном в 1924. Два множества Аи Вв Т. п. наз. функционально отделимыми, если существует определенная на всем пространстве Xдействительная непрерывная и ограниченная на всем Xфункция f, принимающая во всех точках множества Азначение 0 и во всех точках множества Взначение 1. В нормальном пространстве всякие два дизъюнктные замкнутые множества функционально отделимы (лемма Урысона). Обратно, из функциональной отделимости двух любых множеств следует и их отделимость посредством окрестностей. В частности, из функциональной отделимости точки и множества следует их отделимость посредством окрестностей в данном пространстве. Но если пространство регулярно и, значит, всякая точка и всякое не содержащее ее замкнутое множество имеют дизъюнктные окрестности, то отсюда еще не следует, что они функционально отделимы. Таким образом, более сильным, чем свойство регулярности, является свойство полной регулярности пространства, заключающееся в том, что всякая точка и всякое не содержащее ее замкнутое множество в этом пространстве функционально отделимы. Среди удовлетворяющих этому условию (или вполне регулярных) пространств наиболее важны вполне регулярные T1 -пространства, наз. тихоновскими пространствами. В частности, пространство всякой топологич. группы является вполне регулярным, но может не быть нормальным.
Наряду с аксиомами отделимости для всей теории Т. п. имеют значение т. н. условия типа компактности. Они основаны на рассмотрении (открытых) покрытий. Семейство  (открытых) множеств данного Т. п. наз. покрытием этого пространства X, если каждая точка
(открытых) множеств данного Т. п. наз. покрытием этого пространства X, если каждая точка  содержится хотя бы в одном множестве - элементе семейства
содержится хотя бы в одном множестве - элементе семейства  Если каждый элемент покрытия
Если каждый элемент покрытия  является подмножеством хотя бы одного элемента покрытия
является подмножеством хотя бы одного элемента покрытия  то говорят, что
то говорят, что  вписано в
вписано в 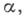 или что
или что  мельче
мельче  или, наконец, что
или, наконец, что  следует за
следует за  в частично упорядоченном множестве покрытий данного пространства. Частным случаем следования покрытия
в частично упорядоченном множестве покрытий данного пространства. Частным случаем следования покрытия  за
за  является случай, когда
является случай, когда  содержится в
содержится в  (т. е. каждый элемент покрытия
(т. е. каждый элемент покрытия  есть и элемент покрытия
есть и элемент покрытия  То или иное условие типа компактности предполагает, что даны два класса (открытых) покрытий пространства X:класс
То или иное условие типа компактности предполагает, что даны два класса (открытых) покрытий пространства X:класс  и класс
и класс  так, что
так, что  т. е. каждое покрытие класса
т. е. каждое покрытие класса  есть и покрытие класса
есть и покрытие класса 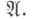 Условие
Условие  -компактности состоит в том, что за каждым покрытием класса
-компактности состоит в том, что за каждым покрытием класса  следует покрытие класса
следует покрытие класса  Важнейшее среди всех условий этого типа получается, если
Важнейшее среди всех условий этого типа получается, если  есть класс всех открытых покрытий пространства, а
есть класс всех открытых покрытий пространства, а  - подкласс конечных покрытий, т. е. покрытий, состоящих из конечного числа элементов. Это условие наз. условием бикомпактности; оно эквивалентно т. <н. условию Бореля - Лебега: для каждого открытого покрытия
- подкласс конечных покрытий, т. е. покрытий, состоящих из конечного числа элементов. Это условие наз. условием бикомпактности; оно эквивалентно т. <н. условию Бореля - Лебега: для каждого открытого покрытия  пространства Xсуществует конечное покрытие
пространства Xсуществует конечное покрытие  пространства X, содержащееся в
пространства X, содержащееся в  Хаусдорфовы пространства, удовлетворяющие условию бикомпактности, наз. бикомпактами. Все они нормальны. Метризуемые бикомпакты (бикомпакты со счетной базой) наз. компактами. В настоящее время получила распространение другая терминология, согласно к-рой бикомпакты наз. компактными Т. п., причем метризуе-мый случай терминологически не выделяется.
Хаусдорфовы пространства, удовлетворяющие условию бикомпактности, наз. бикомпактами. Все они нормальны. Метризуемые бикомпакты (бикомпакты со счетной базой) наз. компактами. В настоящее время получила распространение другая терминология, согласно к-рой бикомпакты наз. компактными Т. п., причем метризуе-мый случай терминологически не выделяется.
Если за  принять класс счетных открытых покрытий, сохраняя в качестве
принять класс счетных открытых покрытий, сохраняя в качестве  подкласс конечных покрытий, то соответствующая
подкласс конечных покрытий, то соответствующая  -компактность наз. счетной компактностью. Для метризуемых пространств, а также для хаусдорфовых пространств со счетной базой условия бикомпактности и счетной компактности эквивалентны между собой. Если за
-компактность наз. счетной компактностью. Для метризуемых пространств, а также для хаусдорфовых пространств со счетной базой условия бикомпактности и счетной компактности эквивалентны между собой. Если за  взять класс всех открытых покрытий, а за
взять класс всех открытых покрытий, а за  - класс счетных покрытий, то получается условие финальной компактности. При формулировке этого условия можно потребовать (как и в случае бикомпактности), чтобы покрытие
- класс счетных покрытий, то получается условие финальной компактности. При формулировке этого условия можно потребовать (как и в случае бикомпактности), чтобы покрытие  не только следовало за покрытием
не только следовало за покрытием  но и содержалось в нем.
но и содержалось в нем.
Важный класс пространств, наз. локально бикомпактными, определяется требованием, чтобы каждая точка хданного пространства X имела окрестность О х, замыкание к-рой в пространстве Xесть бикомпактное подпространство. Всякое локально бикомпактное хаусдорфово пространство и только такое пространство может рассматриваться как открытое множeство нек-рого бикомпакта  причем
причем  получается из X присоединением одной только точки
получается из X присоединением одной только точки  и топология бикомпакта
и топология бикомпакта  однозначно определена последним требованием и топологией пространства X; бикомпакт
однозначно определена последним требованием и топологией пространства X; бикомпакт  наз. одноточечным, или александровским, бикомпактным расширением пространства X.
наз. одноточечным, или александровским, бикомпактным расширением пространства X.
Важнейшим после условия бикомпактности условием типа компактности является условие паракомпактности, требующее, чтобы за всяким открытым покрытием  данного пространства X следовало локально конечное открытое покрытие
данного пространства X следовало локально конечное открытое покрытие 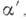 (семейство множеств Т. п. наз. локально конечным в нем, если каждая точка его обладает окрестностью, к-рая может иметь общие точки лишь с конечным числом множеств семейства). Здесь уже нельзя требовать, чтобы
(семейство множеств Т. п. наз. локально конечным в нем, если каждая точка его обладает окрестностью, к-рая может иметь общие точки лишь с конечным числом множеств семейства). Здесь уже нельзя требовать, чтобы 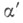 содержалось в
содержалось в  Все метризуемые пространства являются паракомпактными хаусдорфовыми пространствами.
Все метризуемые пространства являются паракомпактными хаусдорфовыми пространствами.
Лит.:[1] Алоксандров П. С., Введение в теорию множеств и общую топологию, М., 1977; [2] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; [3] Куратовский К., Топология, т. 1, [пер. с англ.], М., 1966; [4] Александров П. С., Пасынков Б. А., Введение в теорию размерности..., М., 1973.
П. С. Александров.

 будет пониматься открытая топология. Логически самый простой способ определения топологии в данном множестве Xзаключается в непосредственном указании тех подмножеств множества X, к-рые составляют эту топологию. Но часто проще определять не все множества, являющиеся элементами данной топологии, а только нек-рые множества этих элементов (т. е. базу данной топологии), достаточные для того, чтобы все остальные элементы топологии получались как объединения (в случае открытой топологии) или пересечения (в случае замкнутой) множеств, к-рые составляют базу. Так, напр., обычная топология числовой прямой получается, если определить в качестве базы ее открытой топологии множество всех интервалов (можно ограничиться даже одними интервалами с рациональными концами). Остальные открытые множества суть объединения интервалов.
будет пониматься открытая топология. Логически самый простой способ определения топологии в данном множестве Xзаключается в непосредственном указании тех подмножеств множества X, к-рые составляют эту топологию. Но часто проще определять не все множества, являющиеся элементами данной топологии, а только нек-рые множества этих элементов (т. е. базу данной топологии), достаточные для того, чтобы все остальные элементы топологии получались как объединения (в случае открытой топологии) или пересечения (в случае замкнутой) множеств, к-рые составляют базу. Так, напр., обычная топология числовой прямой получается, если определить в качестве базы ее открытой топологии множество всех интервалов (можно ограничиться даже одними интервалами с рациональными концами). Остальные открытые множества суть объединения интервалов.  порождающую топологию данного Т. п. Метризуемые пространства образуют один из важнейших классов Т. п., и к центральным проблемам общей топологии принадлежали в течение нескольких десятилетий общая и специальная проблемы метризации, т. е. проблемы нахождения необходимых и достаточных условий для того, чтобы Т. п. или Т. п. того или иного специального класса было метризуемым. Эти условия составляют содержание общих или специальных метризационных теорем.
порождающую топологию данного Т. п. Метризуемые пространства образуют один из важнейших классов Т. п., и к центральным проблемам общей топологии принадлежали в течение нескольких десятилетий общая и специальная проблемы метризации, т. е. проблемы нахождения необходимых и достаточных условий для того, чтобы Т. п. или Т. п. того или иного специального класса было метризуемым. Эти условия составляют содержание общих или специальных метризационных теорем.  естественно превращается в Т. п. (подпространство пространства
естественно превращается в Т. п. (подпространство пространства  с топологией, элементы к-рой суть всевозможные множества вида
с топологией, элементы к-рой суть всевозможные множества вида  где Г - любой элемент топологии
где Г - любой элемент топологии  Пусть дана (открытая) топология
Пусть дана (открытая) топология  в множестве X, превращающая это множество в Т. п.. X,
в множестве X, превращающая это множество в Т. п.. X, Т. к. топология есть множество нек-рых подмножеств множества X, то между различными топологиями в одном и том же множестве Xестественно устанавливается отношение (частичного) порядка (по включению), т. е. топология
Т. к. топология есть множество нек-рых подмножеств множества X, то между различными топологиями в одном и том же множестве Xестественно устанавливается отношение (частичного) порядка (по включению), т. е. топология  больше (или равна) топологии
больше (или равна) топологии  если
если  есть подмножество множества
есть подмножество множества  т. е. каждое множество, открытое в топологии
т. е. каждое множество, открытое в топологии  будет открытым и в топологии
будет открытым и в топологии  Если в пределах данного рассуждения речь идет об одной и той же топологии в данном множестве X, то обыкновенно Т. п. X,
Если в пределах данного рассуждения речь идет об одной и той же топологии в данном множестве X, то обыкновенно Т. п. X,  обозначается просто X. Из понятия топологии выводятся и все остальные основные топологич. понятия. Прежде всего замкнутые множества определяются как дополнения к открытым. Далее, окрестностью точки хв данном пространстве . наз. всякое открытое множество, содержащее точку х. Понятие окрестности позволяет сразу же определить и понятие точки прикосновения для любого множества
обозначается просто X. Из понятия топологии выводятся и все остальные основные топологич. понятия. Прежде всего замкнутые множества определяются как дополнения к открытым. Далее, окрестностью точки хв данном пространстве . наз. всякое открытое множество, содержащее точку х. Понятие окрестности позволяет сразу же определить и понятие точки прикосновения для любого множества  как такой точки, любая окрестность к-рой имеет непустое пересечение с множеством М. Из этого определения следует, что любая точка самого множества Мявляется точкой прикосновения этого множества. Множество всех точек прикосновения множества Мназ. замыканием множества Ми обозначается [М].Переход от любого множества Мк его замыканию наз. операцией замыкания в данном Т. п. Свойства этой операции: 1)
как такой точки, любая окрестность к-рой имеет непустое пересечение с множеством М. Из этого определения следует, что любая точка самого множества Мявляется точкой прикосновения этого множества. Множество всех точек прикосновения множества Мназ. замыканием множества Ми обозначается [М].Переход от любого множества Мк его замыканию наз. операцией замыкания в данном Т. п. Свойства этой операции: 1)  причем М=[М]тогда и только тогда, когда Мзамкнуто, т. е. его дополнение открыто;
причем М=[М]тогда и только тогда, когда Мзамкнуто, т. е. его дополнение открыто;  3)
3)  Замыкание любого множества есть пересечение всех замкнутых множеств, содержащих множество М;другими словами, [М]есть наименьшее замкнутое множество, содержащее множество М.
Замыкание любого множества есть пересечение всех замкнутых множеств, содержащих множество М;другими словами, [М]есть наименьшее замкнутое множество, содержащее множество М.  На основе так введенного понятия замыкания замкнутые множества определятся как множества, совпадающие со своими замыканиями, а открытые множества - как множества, дополнительные к замкнутым; таким образом получается в точности топология в нашем первоначальном смысле, а операция замыкания, к к-рой она приводит, совпадает с той, к-рая была дана априори. Именно этот путь и был избран К. Куратовским (К. Кuratowski, 1922) для построения понятия Т. п. В 1925 II. С. Александровым были введены открытые топологич. структуры. Оба подхода приводят к одному и тому же классу Т. п., в настоящее время являющемуся общепринятым.
На основе так введенного понятия замыкания замкнутые множества определятся как множества, совпадающие со своими замыканиями, а открытые множества - как множества, дополнительные к замкнутым; таким образом получается в точности топология в нашем первоначальном смысле, а операция замыкания, к к-рой она приводит, совпадает с той, к-рая была дана априори. Именно этот путь и был избран К. Куратовским (К. Кuratowski, 1922) для построения понятия Т. п. В 1925 II. С. Александровым были введены открытые топологич. структуры. Оба подхода приводят к одному и тому же классу Т. п., в настоящее время являющемуся общепринятым.  Т. п. Xв Т. п. Yнепрерывно в точке
Т. п. Xв Т. п. Yнепрерывно в точке  если для любой окрестности О у точки
если для любой окрестности О у точки  в пространстве Yсуществует такая окрестность О х точки хв X, что
в пространстве Yсуществует такая окрестность О х точки хв X, что  (условие Коши). При этом, не изменяя содержания определения, можно брать окрестности О у и О х из любых открытых баз соответственно пространств Yи X. В частности, для метрич. пространств это определение непрерывности переходит в обычное известное из курсов математич. анализа определение. Если отображение
(условие Коши). При этом, не изменяя содержания определения, можно брать окрестности О у и О х из любых открытых баз соответственно пространств Yи X. В частности, для метрич. пространств это определение непрерывности переходит в обычное известное из курсов математич. анализа определение. Если отображение  непрерывно в каждой точке
непрерывно в каждой точке  то оно наз. непрерывным отображением пространства X в пространство Y. Для непрерывности отображения
то оно наз. непрерывным отображением пространства X в пространство Y. Для непрерывности отображения  каждое из следующих условий необходимо и достаточно. 1) Если хесть точка прикосновения какого-либо множества
каждое из следующих условий необходимо и достаточно. 1) Если хесть точка прикосновения какого-либо множества  то f(x)есть точка прикосновения множества f(M)в F. 2) Полный прообраз f-1 (Г) всякого открытого в У множества Г есть открытое множество в X. Аналогично для замкнутых множеств.
то f(x)есть точка прикосновения множества f(M)в F. 2) Полный прообраз f-1 (Г) всякого открытого в У множества Г есть открытое множество в X. Аналогично для замкнутых множеств.  на подпространство Х 0) также непрерывно.
на подпространство Х 0) также непрерывно.  открыто (замкнуто) в У тогда и только тогда, когда f-1(B) обладает тем же свойством в X. Если непрерывное отображение f пространства Xна пространство У взаимно однозначно, то определено и обратное отображение
открыто (замкнуто) в У тогда и только тогда, когда f-1(B) обладает тем же свойством в X. Если непрерывное отображение f пространства Xна пространство У взаимно однозначно, то определено и обратное отображение  но это отображение может не быть непрерывным. Если же оно непрерывно, то каждое из отображений f, f-1 взаимно однозначно отображает топологию одного из пространств X, Y на топологию другого пространства. Тогда каждое из двух взаимно однозначных отображений f и f-l наз. топологическим отображением, или гомеомоpфизмом. Два пространства X и Y, из к-рых одно может быть гомеоморфно отображено на другое, наз. гомеоморфными или топологически эквивалентными между собою.
но это отображение может не быть непрерывным. Если же оно непрерывно, то каждое из отображений f, f-1 взаимно однозначно отображает топологию одного из пространств X, Y на топологию другого пространства. Тогда каждое из двух взаимно однозначных отображений f и f-l наз. топологическим отображением, или гомеомоpфизмом. Два пространства X и Y, из к-рых одно может быть гомеоморфно отображено на другое, наз. гомеоморфными или топологически эквивалентными между собою.  наз. неприводимым, если при этом отображении никакое отличное от всего Xзамкнутое множество Мне отображается на все Y.
наз. неприводимым, если при этом отображении никакое отличное от всего Xзамкнутое множество Мне отображается на все Y.  получает топологию, однозначно определенную топологией
получает топологию, однозначно определенную топологией  и таким образом становится топологич. подпространством пространства X,
и таким образом становится топологич. подпространством пространства X, При этом всякое подпространство пространства, удовлетворяющего аксиоме Ti, i=0, 1, 2, 3, также удовлетворяет аксиоме Т i, т. е. аксиомы Ti наследуются всеми подпространствами данного пространства. Аксиома Т 4 этим свойством не обладает: существуют нормальные пространства X, не все (даже открытые в X)подпространства к-рых нормальны. Однако если Х 0 -замкнутое множество в нормальном пространстве X, то подпространство Х 0 нормально.
При этом всякое подпространство пространства, удовлетворяющего аксиоме Ti, i=0, 1, 2, 3, также удовлетворяет аксиоме Т i, т. е. аксиомы Ti наследуются всеми подпространствами данного пространства. Аксиома Т 4 этим свойством не обладает: существуют нормальные пространства X, не все (даже открытые в X)подпространства к-рых нормальны. Однако если Х 0 -замкнутое множество в нормальном пространстве X, то подпространство Х 0 нормально.  (открытых) множеств данного Т. п. наз. покрытием этого пространства X, если каждая точка
(открытых) множеств данного Т. п. наз. покрытием этого пространства X, если каждая точка  содержится хотя бы в одном множестве - элементе семейства
содержится хотя бы в одном множестве - элементе семейства  Если каждый элемент покрытия
Если каждый элемент покрытия  является подмножеством хотя бы одного элемента покрытия
является подмножеством хотя бы одного элемента покрытия  то говорят, что
то говорят, что  вписано в
вписано в 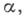 или что
или что  мельче
мельче  или, наконец, что
или, наконец, что  следует за
следует за  в частично упорядоченном множестве покрытий данного пространства. Частным случаем следования покрытия
в частично упорядоченном множестве покрытий данного пространства. Частным случаем следования покрытия  за
за  является случай, когда
является случай, когда  содержится в
содержится в  (т. е. каждый элемент покрытия
(т. е. каждый элемент покрытия  есть и элемент покрытия
есть и элемент покрытия  То или иное условие типа компактности предполагает, что даны два класса (открытых) покрытий пространства X:класс
То или иное условие типа компактности предполагает, что даны два класса (открытых) покрытий пространства X:класс  и класс
и класс  так, что
так, что  т. е. каждое покрытие класса
т. е. каждое покрытие класса  есть и покрытие класса
есть и покрытие класса 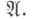 Условие
Условие  -компактности состоит в том, что за каждым покрытием класса
-компактности состоит в том, что за каждым покрытием класса  следует покрытие класса
следует покрытие класса  Важнейшее среди всех условий этого типа получается, если
Важнейшее среди всех условий этого типа получается, если  есть класс всех открытых покрытий пространства, а
есть класс всех открытых покрытий пространства, а  - подкласс конечных покрытий, т. е. покрытий, состоящих из конечного числа элементов. Это условие наз. условием бикомпактности; оно эквивалентно т. <н. условию Бореля - Лебега: для каждого открытого покрытия
- подкласс конечных покрытий, т. е. покрытий, состоящих из конечного числа элементов. Это условие наз. условием бикомпактности; оно эквивалентно т. <н. условию Бореля - Лебега: для каждого открытого покрытия  пространства Xсуществует конечное покрытие
пространства Xсуществует конечное покрытие  пространства X, содержащееся в
пространства X, содержащееся в  Хаусдорфовы пространства, удовлетворяющие условию бикомпактности, наз. бикомпактами. Все они нормальны. Метризуемые бикомпакты (бикомпакты со счетной базой) наз. компактами. В настоящее время получила распространение другая терминология, согласно к-рой бикомпакты наз. компактными Т. п., причем метризуе-мый случай терминологически не выделяется.
Хаусдорфовы пространства, удовлетворяющие условию бикомпактности, наз. бикомпактами. Все они нормальны. Метризуемые бикомпакты (бикомпакты со счетной базой) наз. компактами. В настоящее время получила распространение другая терминология, согласно к-рой бикомпакты наз. компактными Т. п., причем метризуе-мый случай терминологически не выделяется.  принять класс счетных открытых покрытий, сохраняя в качестве
принять класс счетных открытых покрытий, сохраняя в качестве  подкласс конечных покрытий, то соответствующая
подкласс конечных покрытий, то соответствующая  -компактность наз. счетной компактностью. Для метризуемых пространств, а также для хаусдорфовых пространств со счетной базой условия бикомпактности и счетной компактности эквивалентны между собой. Если за
-компактность наз. счетной компактностью. Для метризуемых пространств, а также для хаусдорфовых пространств со счетной базой условия бикомпактности и счетной компактности эквивалентны между собой. Если за  взять класс всех открытых покрытий, а за
взять класс всех открытых покрытий, а за  - класс счетных покрытий, то получается условие финальной компактности. При формулировке этого условия можно потребовать (как и в случае бикомпактности), чтобы покрытие
- класс счетных покрытий, то получается условие финальной компактности. При формулировке этого условия можно потребовать (как и в случае бикомпактности), чтобы покрытие  не только следовало за покрытием
не только следовало за покрытием  но и содержалось в нем.
но и содержалось в нем.  причем
причем  получается из X присоединением одной только точки
получается из X присоединением одной только точки  и топология бикомпакта
и топология бикомпакта  однозначно определена последним требованием и топологией пространства X; бикомпакт
однозначно определена последним требованием и топологией пространства X; бикомпакт  наз. одноточечным, или александровским, бикомпактным расширением пространства X.
наз. одноточечным, или александровским, бикомпактным расширением пространства X.  данного пространства X следовало локально конечное открытое покрытие
данного пространства X следовало локально конечное открытое покрытие 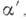 (семейство множеств Т. п. наз. локально конечным в нем, если каждая точка его обладает окрестностью, к-рая может иметь общие точки лишь с конечным числом множеств семейства). Здесь уже нельзя требовать, чтобы
(семейство множеств Т. п. наз. локально конечным в нем, если каждая точка его обладает окрестностью, к-рая может иметь общие точки лишь с конечным числом множеств семейства). Здесь уже нельзя требовать, чтобы 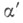 содержалось в
содержалось в  Все метризуемые пространства являются паракомпактными хаусдорфовыми пространствами.
Все метризуемые пространства являются паракомпактными хаусдорфовыми пространствами.