"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОНКИЙ ПУЧОКЗначение ТОНКИЙ ПУЧОК в математической энциклопедии:
- пучок абелевых групп  на паракомпактном пространстве X, пучок эндоморфизмов к-рого есть мягкий пучок. Пучок на паракомпактном пространстве X, пучок эндоморфизмов к-рого есть мягкий пучок. Пучок  является Т. п. тогда и только тогда, когда для любых замкнутых подмножеств является Т. п. тогда и только тогда, когда для любых замкнутых подмножеств  таких, что таких, что  существует эндоморфизм существует эндоморфизм 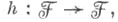 тождественный над Аи равный 0 над В, или когда для любого открытого покрытия тождественный над Аи равный 0 над В, или когда для любого открытого покрытия  пространства Xсуществует такое локально конечное семейство пространства Xсуществует такое локально конечное семейство  эндоморфизмов пучка эндоморфизмов пучка  что supp что supp  и и  - тождественный эндоморфизм. Всякий Т. п. является мягким, а если - тождественный эндоморфизм. Всякий Т. п. является мягким, а если  - пучок колец с единицами, то верно и обратное. Если - пучок колец с единицами, то верно и обратное. Если  - Т. п., а - Т. п., а  - любой пучок абелевых групп на X, то - любой пучок абелевых групп на X, то  - также Т. п. Примером Т. п. служит пучок ростков непрерывных (или дифференцируемых класса С k) сечений произвольного (соответственно дифференцируемого) векторного расслоения над паракомпактным пространством (соответственно паракомпактным дифференцируемым многообразием). - также Т. п. Примером Т. п. служит пучок ростков непрерывных (или дифференцируемых класса С k) сечений произвольного (соответственно дифференцируемого) векторного расслоения над паракомпактным пространством (соответственно паракомпактным дифференцируемым многообразием). Лит.:[1] Годеман Р., Алгебраическая топология и теория пучков, пер. с франц., М., 1961; [2] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976.
А. Л. Онищик.
|

 на паракомпактном пространстве X, пучок эндоморфизмов к-рого есть мягкий пучок. Пучок
на паракомпактном пространстве X, пучок эндоморфизмов к-рого есть мягкий пучок. Пучок  является Т. п. тогда и только тогда, когда для любых замкнутых подмножеств
является Т. п. тогда и только тогда, когда для любых замкнутых подмножеств  таких, что
таких, что  существует эндоморфизм
существует эндоморфизм 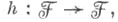 тождественный над Аи равный 0 над В, или когда для любого открытого покрытия
тождественный над Аи равный 0 над В, или когда для любого открытого покрытия  пространства Xсуществует такое локально конечное семейство
пространства Xсуществует такое локально конечное семейство  эндоморфизмов пучка
эндоморфизмов пучка  что supp
что supp  и
и  - тождественный эндоморфизм. Всякий Т. п. является мягким, а если
- тождественный эндоморфизм. Всякий Т. п. является мягким, а если  - пучок колец с единицами, то верно и обратное. Если
- пучок колец с единицами, то верно и обратное. Если  - Т. п., а
- Т. п., а  - любой пучок абелевых групп на X, то
- любой пучок абелевых групп на X, то  - также Т. п. Примером Т. п. служит пучок ростков непрерывных (или дифференцируемых класса С k) сечений произвольного (соответственно дифференцируемого) векторного расслоения над паракомпактным пространством (соответственно паракомпактным дифференцируемым многообразием).
- также Т. п. Примером Т. п. служит пучок ростков непрерывных (или дифференцируемых класса С k) сечений произвольного (соответственно дифференцируемого) векторного расслоения над паракомпактным пространством (соответственно паракомпактным дифференцируемым многообразием).