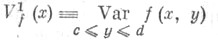" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ТОНЕЛЛИ ПЛОСКАЯ ВАРИАЦИЯ

Значение ТОНЕЛЛИ ПЛОСКАЯ ВАРИАЦИЯ в математической энциклопедии:

числовая характеристика функции двух переменных, с помощью к-рой определяется класс функций, имеющих ограниченную вариацию в смысле Тонелли. Пусть функция f(x, у )задана на прямоугольнике Предполагается, что функции

и

измеримы по Лебегу (первая - на отрезке [ а, b],вторая - на [ с, d]).Если

то говорят, что функция f(x, у )имеет ограниченную (конечную) плоскую вариацию Тонелли на прямоугольнике D, а класс всех таких функций обозначают T(D). Это определение предложено Л. Тонелли (см. [1], [2]). Однако для непрерывных функций f(x, у )другая характеристика класса Т(D)(в терминах Банаха индикатрисы) содержится в более ранней работе С. Банаха [4]. Если функция f(x, у )непрерывна на прямоугольнике D, то для того чтобы поверхность z=f(x, у )имела конечную площадь, необходимо и достаточно, чтобы функция f( х, у )принадлежала классу T(D).

Лит.:[1] Tonelli L., лС. r. Acad. sci.