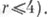"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТОМА КАТАСТРОФЫЗначение ТОМА КАТАСТРОФЫ в математической энциклопедии:
- особенности дифференцируемых отображений, классификация к-рых была анонсирована Р. Томом [1] при рассмотрении им градиентных динамич. систем и аналогичная списку критических точек коразмерности 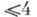 дифференцируемых функций. Исходная формулировка результата Тома: 4-параметрические семейства функций в типичном случае устойчивы и с точностью до знака и замены переменных задаются в окрестности критич. точки одним из семи выражений (см. табл.). дифференцируемых функций. Исходная формулировка результата Тома: 4-параметрические семейства функций в типичном случае устойчивы и с точностью до знака и замены переменных задаются в окрестности критич. точки одним из семи выражений (см. табл.).
| Обозначение | Коразмерность | Коранг | Росток | Универсальная деформация | Название | | A2 | 1 | 1 | х 3 + у2 | их | Складка | | А 3 | 2 | 1 | х 4 + у2 | ux + vx2 | Сборка | | А 4 | 3 | 1 | х 5 + у2 | их + vx2 + их3 | Ласточкин | | D-4 | 3 | 2 | х 3 + ху2 | ux + vx2 + wy | Гиперболич. омбилика | | D+4 | 3 | 2 | х 3 - ху2 | ux+vx2 + wy | Эллиптич. омбилика | | А 5 | 4 | 2 | x6 + у2 | ux + vx2 + +wx3+ tx4 | Бабочка | | D5 | 4 | 2 | х 4 + ху 2 | ux + vx2 + + wx3 + ty | Парабол ич. омбилика | Ростки, отвечающие Т. к., являются конечно определенными (точнее, 6-определенными: в подходящих координатах они записываются как многочлены от двух переменных степени 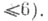
Коразмерность codim служит мерой сложности критич. точек; любое достаточно малое возмущение функции f с codim-r приводит к функции, имеющей не более r критич. точки. Коразмерностью особенности (т. <е. ростка f, для к-рого f(0)=Df(0)=0) наз. число  где где  - идеал, порожденный ростками - идеал, порожденный ростками  Напр., если f=xN, то Напр., если f=xN, то 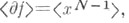 и базисом и базисом 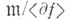 служат смежные классы элементов х, х2, . . ., xN-2, так что codim=2. служат смежные классы элементов х, х2, . . ., xN-2, так что codim=2.
Имеет место неравенство codim  где с - коранг гессиана где с - коранг гессиана  отсюда, в частности, если отсюда, в частности, если  то то 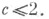
Конечная определенность (достаточность) ростка, грубо говоря, означает, что он определяется с точностью до гладких замен координат своей струей. Точнее, росток f наз. k-определенным, если каждый росток f', имеющий ту же k-струю (т. е. отрезок ряда Тейлора до членов порядка 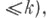 что и f, правоэквивалентен f (см. |2]). Для конечной определенности ростка необходима и достаточна конечность его коразмерности. В частности, если codim=r, то f является (r+2)-определенным (отсюда 6-определенности при что и f, правоэквивалентен f (см. |2]). Для конечной определенности ростка необходима и достаточна конечность его коразмерности. В частности, если codim=r, то f является (r+2)-определенным (отсюда 6-определенности при 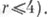
Т. к., в отличие от случая общего положения, являются вырожденными особенностями (т. е. гессиан в них вырожден), и от них можно, как указывалось, избавиться малым возмущением. Однако для многих практически важных случаев, равно как и в теоретич. плане, представляет интерес не индивидуальный объект, а семейство таковых, зависящее от нескольких луправляющих
|

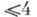 дифференцируемых функций. Исходная формулировка результата Тома: 4-параметрические семейства функций в типичном случае устойчивы и с точностью до знака и замены переменных задаются в окрестности критич. точки одним из семи выражений (см. табл.).
дифференцируемых функций. Исходная формулировка результата Тома: 4-параметрические семейства функций в типичном случае устойчивы и с точностью до знака и замены переменных задаются в окрестности критич. точки одним из семи выражений (см. табл.). 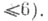
 где
где  - идеал, порожденный ростками
- идеал, порожденный ростками  Напр., если f=xN, то
Напр., если f=xN, то 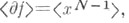 и базисом
и базисом 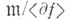 служат смежные классы элементов х, х2, . . ., xN-2, так что codim=2.
служат смежные классы элементов х, х2, . . ., xN-2, так что codim=2.  где с - коранг гессиана
где с - коранг гессиана  отсюда, в частности, если
отсюда, в частности, если  то
то 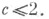
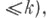 что и f, правоэквивалентен f (см. |2]). Для конечной определенности ростка необходима и достаточна конечность его коразмерности. В частности, если codim=r, то f является (r+2)-определенным (отсюда 6-определенности при
что и f, правоэквивалентен f (см. |2]). Для конечной определенности ростка необходима и достаточна конечность его коразмерности. В частности, если codim=r, то f является (r+2)-определенным (отсюда 6-определенности при