|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БОРЕЛЕВСКАЯ СИСТЕМА МНОЖЕСТВЗначение БОРЕЛЕВСКАЯ СИСТЕМА МНОЖЕСТВ в математической энциклопедии: (В - система), порожденная системой множеств М,- наименьшая (s,d)-система множеств В(М), содержащая М. Множества Б. с. м. В(М).наз. борелевскими множествами (или В- множествами), порожденными системой М. Для каждого порядкового числа А. Г. Елъкин. |
|
|
|
(
- начальное порядковое число мощности 
) следующим образом определяются борелевские классы 
при нечетном а состоит из объединений, а при четном 
- из пересечений последовательностей множеств, принадлежащих 
Тогда 
Видоизмененное построение Б. с. м. В(М).получится, если поменять ролями операции пересечения и объединения. Борелевское множество принадлежит в точности классу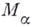 
, если оно принадлежит 
, но не принадлежит 
при 
(иногда считают классы непересекающимися, т. е. наз. классом систему 
.