|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТЕТРАЦИКЛИЧЕСКИЕ КООРДИНАТЫЗначение ТЕТРАЦИКЛИЧЕСКИЕ КООРДИНАТЫ в математической энциклопедии: точки на плоскости - четыре числа х 1, ,x2, х3, x4, подчиненные равенствам
Можно ввести Т. к. и для круга на плоскости. При указанном специальном выборе четырех основных кругов круг с центром в точке
Т. к. точек и кругов на плоскости можно ввести с помощью стереографической проекции. При этом Т. к. точки на плоскости - однородные координаты соответствующей при стереографич. проектировании точки на сфере. Т. к. круга на плоскости - однородные координаты точки пространства, являющейся полюсом плоскости круга на сфере, соответствующего в стереографич. проекции кругу на плоскости, относительно этой сферы. Лит.:[1] Клейн Ф., Высшая геометрия, пер. с нем., М.-Л., 1939; [2] Бушманова Г. В., Норден А. II., Элементы конформной геометрии, Казань, 1972. |
|
|
|

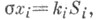 i=l, 2, 3, 4, где Si -
i=l, 2, 3, 4, где Si - 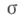 - множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду
- множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду 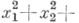
 если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы
если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы  i=1, 2, 3, и одна - мнимый
i=1, 2, 3, и одна - мнимый  а числа ki равными
а числа ki равными  Если в плоскости ввести декартовы координаты
Если в плоскости ввести декартовы координаты 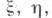 а в качестве трех действительных кругов взять
а в качестве трех действительных кругов взять  (круги, проходящие через бесконечно удаленную точку плоскости), круг
(круги, проходящие через бесконечно удаленную точку плоскости), круг 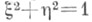 и мнимый круг
и мнимый круг  то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом:
то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом: 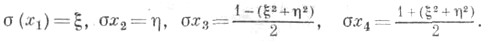
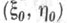 и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами
и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами 