"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТЕТА-ФУНКЦИЯ
Значение ТЕТА-ФУНКЦИЯ в математической энциклопедии:
, ТЕТА-ФУНКЦИЯ  -функция, одного комплексного переменного - квазидвоякопериодическая целая функция комплексного переменного z, т. е. функция
-функция, одного комплексного переменного - квазидвоякопериодическая целая функция комплексного переменного z, т. е. функция  имеющая, кроме периода
имеющая, кроме периода  еще квазипериод
еще квазипериод  при прибавлении к-poro к значению аргумента значение функции умножается на нек-рый мультипликатор. Иначе говоря, имеют место тождества по z:
при прибавлении к-poro к значению аргумента значение функции умножается на нек-рый мультипликатор. Иначе говоря, имеют место тождества по z:

Как периодическая целая функция, Т.-ф. всегда представима рядом

в к-ром подбор коэффициентов с п должен обеспечивать сходимость. Ряды (1) наз. тета-рядами (по причине первоначальных обозначений). Возможны и иные представления Т.-ф., напр. в виде бесконечного произведения.
В приложениях обычно ограничиваются мультипликаторами вида
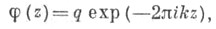
где k- натуральное число, называемое порядком или весом Т.-ф., q - числовой множитель, Сходимость обеспечивается, напр., коэффициентами вида

Во многих вопросах удобны Т.-ф., удовлетворяющие условиям

Все Т.-ф. вида (2) одного и того же порядка kсоставляют векторное пространство размерности k. Базис этого пространства можно записать в виде

Отдельные примеры Т.-ф. встречаются уже в работах Я. Бернулли (J. Bernoulli, 1713), Л. Эйлера (L. Euler), в теории теплопроводности Ж. Фурье (J. Fourier).
К. Якоби (С. Jacobi) подверг Т.-ф. системaтич. исследованию, выделил четыре специальные Т.-ф., к-рые и положил в основу своей теории эллиптич. функций (см. Якоби эллиптические функции).
Т.-ф. нескольких комплексных переменных возникают как естественное обобщение Т.-ф. одного комплексного переменного. Они строятся следующим образом. Пусть z=(z1, . . ., zp) - матрица-строка ркомплексных переменных,  есть
есть  -я строка единичной матрицы Епорядка р; п= (п 1, . . ., п р) - целочисленная матрица-строка;
-я строка единичной матрицы Епорядка р; п= (п 1, . . ., п р) - целочисленная матрица-строка; 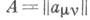 -симметрич. матрица порядка р, составленная из комплексных чисел и такая, что матрица
-симметрич. матрица порядка р, составленная из комплексных чисел и такая, что матрица  порождает положительно определенную квадратичную форму
порождает положительно определенную квадратичную форму  (здесь
(здесь  - транспонированная матрица п). Кратный тета - ряд
- транспонированная матрица п). Кратный тета - ряд

сходится абсолютно и равномерно на компактах из  и определяет, следовательно, целую трансцендентную функцию ркомплексных переменных z1, . . ., zp, называемую тета-функциен порядка 1. Различные элементы матрицы Аназ. модулями, или параметрами Т.-ф.
и определяет, следовательно, целую трансцендентную функцию ркомплексных переменных z1, . . ., zp, называемую тета-функциен порядка 1. Различные элементы матрицы Аназ. модулями, или параметрами Т.-ф.  число модулей равно р(р+1)/2. Т.-ф.
число модулей равно р(р+1)/2. Т.-ф.  1-го порядка удовлетворяет следующим основным тождествам по z:
1-го порядка удовлетворяет следующим основным тождествам по z:

где  v=l, . . ., р;
v=l, . . ., р;  при
при  и
и  при
при  Матрица S=(E, А )размера
Матрица S=(E, А )размера  является системой модулей, или системой периодов и квазипериодов, Т.-ф.
является системой модулей, или системой периодов и квазипериодов, Т.-ф.  Если m=(m1, . . . .. ., т р), т' =( т'1, . . ., т' р) - произвольные целочисленные матрицы-строки, то в более общем виде свойства периодичности Т.-ф. можно записать так:
Если m=(m1, . . . .. ., т р), т' =( т'1, . . ., т' р) - произвольные целочисленные матрицы-строки, то в более общем виде свойства периодичности Т.-ф. можно записать так:

Пусть 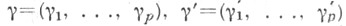 - произвольные комплексные матрицы-строки,
- произвольные комплексные матрицы-строки,  - матрица размера
- матрица размера  Тогда формула
Тогда формула

определяет Т.-ф. 1-го порядка с характеристикой (общего вида) Г; в этой терминологии Т.-ф. (3) имеет характеристику 0. Матрица Г иначе наз. периодич. характеристикой матрицы  Всегда
Всегда  Свойства (4) для Т.-ф. с характеристикой Г обобщаются в виде
Свойства (4) для Т.-ф. с характеристикой Г обобщаются в виде

Характеристика наз. нормальной, если 

Наиболее употребительны дробные характеристики, когда все  - неотрицательные правильные рациональные дроби с общим знаменателем
- неотрицательные правильные рациональные дроби с общим знаменателем  Наиболее важный и простой случай - полуцелые, или половинные, характеристики, когда
Наиболее важный и простой случай - полуцелые, или половинные, характеристики, когда  Полуцелые характеристики
Полуцелые характеристики  можно считать составленными из чисел 0 и 1 (обычно под лтета-характеристиками
можно считать составленными из чисел 0 и 1 (обычно под лтета-характеристиками

 -функция, одного комплексного переменного - квазидвоякопериодическая целая функция комплексного переменного z, т. е. функция
-функция, одного комплексного переменного - квазидвоякопериодическая целая функция комплексного переменного z, т. е. функция  имеющая, кроме периода
имеющая, кроме периода  еще квазипериод
еще квазипериод  при прибавлении к-poro к значению аргумента значение функции умножается на нек-рый мультипликатор. Иначе говоря, имеют место тождества по z:
при прибавлении к-poro к значению аргумента значение функции умножается на нек-рый мультипликатор. Иначе говоря, имеют место тождества по z: 

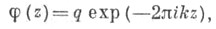



 есть
есть  -я строка единичной матрицы Епорядка р; п= (п 1, . . ., п р) - целочисленная матрица-строка;
-я строка единичной матрицы Епорядка р; п= (п 1, . . ., п р) - целочисленная матрица-строка; 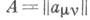 -симметрич. матрица порядка р, составленная из комплексных чисел и такая, что матрица
-симметрич. матрица порядка р, составленная из комплексных чисел и такая, что матрица  порождает положительно определенную квадратичную форму
порождает положительно определенную квадратичную форму  (здесь
(здесь  - транспонированная матрица п). Кратный тета - ряд
- транспонированная матрица п). Кратный тета - ряд 
 и определяет, следовательно, целую трансцендентную функцию ркомплексных переменных z1, . . ., zp, называемую тета-функциен порядка 1. Различные элементы матрицы Аназ. модулями, или параметрами Т.-ф.
и определяет, следовательно, целую трансцендентную функцию ркомплексных переменных z1, . . ., zp, называемую тета-функциен порядка 1. Различные элементы матрицы Аназ. модулями, или параметрами Т.-ф.  число модулей равно р(р+1)/2. Т.-ф.
число модулей равно р(р+1)/2. Т.-ф.  1-го порядка удовлетворяет следующим основным тождествам по z:
1-го порядка удовлетворяет следующим основным тождествам по z: 
 v=l, . . ., р;
v=l, . . ., р;  при
при  и
и  при
при  Матрица S=(E, А )размера
Матрица S=(E, А )размера  является системой модулей, или системой периодов и квазипериодов, Т.-ф.
является системой модулей, или системой периодов и квазипериодов, Т.-ф.  Если m=(m1, . . . .. ., т р), т' =( т'1, . . ., т' р) - произвольные целочисленные матрицы-строки, то в более общем виде свойства периодичности Т.-ф. можно записать так:
Если m=(m1, . . . .. ., т р), т' =( т'1, . . ., т' р) - произвольные целочисленные матрицы-строки, то в более общем виде свойства периодичности Т.-ф. можно записать так: 
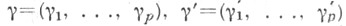 - произвольные комплексные матрицы-строки,
- произвольные комплексные матрицы-строки,  - матрица размера
- матрица размера  Тогда формула
Тогда формула 
 Всегда
Всегда  Свойства (4) для Т.-ф. с характеристикой Г обобщаются в виде
Свойства (4) для Т.-ф. с характеристикой Г обобщаются в виде 


 - неотрицательные правильные рациональные дроби с общим знаменателем
- неотрицательные правильные рациональные дроби с общим знаменателем  Наиболее важный и простой случай - полуцелые, или половинные, характеристики, когда
Наиболее важный и простой случай - полуцелые, или половинные, характеристики, когда  Полуцелые характеристики
Полуцелые характеристики  можно считать составленными из чисел 0 и 1 (обычно под лтета-характеристиками
можно считать составленными из чисел 0 и 1 (обычно под лтета-характеристиками