"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТЕТА-РЯД
Значение ТЕТА-РЯД в математической энциклопедии:
,ТЕТА-РЯД  -ряд,- функциональный ряд, применяемый для представления автоморфных форм и автоморфных функций.
-ряд,- функциональный ряд, применяемый для представления автоморфных форм и автоморфных функций.
Пусть D - область комплексного пространства 
 - дискретная группа автоморфизмов области D. Если группа Г конечна, то из любой мероморфной в Dфункции Н(z), z=(z1, . . ., zp), можно получить автоморфную функцию
- дискретная группа автоморфизмов области D. Если группа Г конечна, то из любой мероморфной в Dфункции Н(z), z=(z1, . . ., zp), можно получить автоморфную функцию

Для бесконечных групп необходимы множители сходимости, что н приводит к Т.-р. Тета-рядом Пуанкаре, или просто рядом Пуанкаре, ассоциированным с группой Г, наз. ряд вида
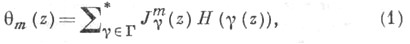
где  - якобиан отображения
- якобиан отображения  т - целое действительное число, называемое весом или порядком; звездочка означает, что суммирование выполняется только по тем
т - целое действительное число, называемое весом или порядком; звездочка означает, что суммирование выполняется только по тем  к-рые доставляют различные члены ряда. При отображении
к-рые доставляют различные члены ряда. При отображении 
 функция
функция  преобразуется по закону
преобразуется по закону  и, следовательно, представляет собой автоморфную функцию веса т, ассоциированную с группой Г. Отношение двух Т.-р. одинакового веса дает автоморфную функцию.
и, следовательно, представляет собой автоморфную функцию веса т, ассоциированную с группой Г. Отношение двух Т.-р. одинакового веса дает автоморфную функцию.
Т.-р. частного вида

наз. тета-рядами Эйзенштейна или просто рядами Эйзенштейна, ассоциированными с группой Г.
Л. Пуанкаре (Н. Poincarе) в серии работ 80-х гг. 19 в. развил теорию Т.-р. в связи с изучением автоморфных функций одного комплексного неременного. Пусть Г - дискретная фуксова группа дробно-линейных преобразований

отображающая единичную окружность на себя, D={z; |z|<1} -единичный круг. Ряды Пуанкаре в этом случае имеют вид

где Н, напр.,- ограниченная голоморфная функция в D. В предположении, что Г действует свободно на Dи фактор Х=D/ Гкомпактен, доказано, что ряд (2) сходится абсолютно и равномерно внутри Dпри  При высказанных условиях на H и Г это утверждение верно и для рядов (1) в случае, когда D- ограниченная область в
При высказанных условиях на H и Г это утверждение верно и для рядов (1) в случае, когда D- ограниченная область в  Для нек-рых фуксовых групп ряды (2) сходятся и при т=1.
Для нек-рых фуксовых групп ряды (2) сходятся и при т=1.
Название лтета-ряды

 -ряд,- функциональный ряд, применяемый для представления автоморфных форм и автоморфных функций.
-ряд,- функциональный ряд, применяемый для представления автоморфных форм и автоморфных функций. 
 - дискретная группа автоморфизмов области D. Если группа Г конечна, то из любой мероморфной в Dфункции Н(z), z=(z1, . . ., zp), можно получить автоморфную функцию
- дискретная группа автоморфизмов области D. Если группа Г конечна, то из любой мероморфной в Dфункции Н(z), z=(z1, . . ., zp), можно получить автоморфную функцию 
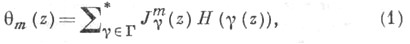
 - якобиан отображения
- якобиан отображения  т - целое действительное число, называемое весом или порядком; звездочка означает, что суммирование выполняется только по тем
т - целое действительное число, называемое весом или порядком; звездочка означает, что суммирование выполняется только по тем  к-рые доставляют различные члены ряда. При отображении
к-рые доставляют различные члены ряда. При отображении 
 функция
функция  преобразуется по закону
преобразуется по закону  и, следовательно, представляет собой автоморфную функцию веса т, ассоциированную с группой Г. Отношение двух Т.-р. одинакового веса дает автоморфную функцию.
и, следовательно, представляет собой автоморфную функцию веса т, ассоциированную с группой Г. Отношение двух Т.-р. одинакового веса дает автоморфную функцию. 


 При высказанных условиях на H и Г это утверждение верно и для рядов (1) в случае, когда D- ограниченная область в
При высказанных условиях на H и Г это утверждение верно и для рядов (1) в случае, когда D- ограниченная область в  Для нек-рых фуксовых групп ряды (2) сходятся и при т=1.
Для нек-рых фуксовых групп ряды (2) сходятся и при т=1.