"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ТАУБЕРОВЫ ТЕОРЕМЫ
Значение ТАУБЕРОВЫ ТЕОРЕМЫ в математической энциклопедии:
теоремы тауберова типа,- теоремы, устанавливающие условия, определяющие множество рядов (или последовательностей), на к-ром для двух данных суммирования методов А и В происходит включение  Наиболее часто в теории суммирования рассматривается случай, когда метод Втождествен сходимости. В Т. т., относящихся к этим случаям, устанавливаются условия на ряд (последовательность), при к-рых из суммируемости ряда данным методом следует его сходимость. Назв. теорем восходит к А. Тауберу [1], впервые доказавшему две теоремы такого тина для Абеля метода суммирования:
Наиболее часто в теории суммирования рассматривается случай, когда метод Втождествен сходимости. В Т. т., относящихся к этим случаям, устанавливаются условия на ряд (последовательность), при к-рых из суммируемости ряда данным методом следует его сходимость. Назв. теорем восходит к А. Тауберу [1], впервые доказавшему две теоремы такого тина для Абеля метода суммирования:
1) если ряд

суммируем методом Абеля к сумме Sи 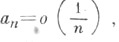 то ряд сходится к S;
то ряд сходится к S;
2) для того чтобы из суммируемости ряда (*) методом Абеля к сумме Sследовала сходимость этого ряда к сумме S, необходимо и достаточно, чтобы
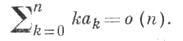
Теорема 1) была позднее усилена, а именно, было показано, что условие 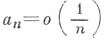 можно заменить на
можно заменить на 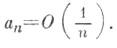 Условия, к-рые накладываются на ряд в этих случаях, помимо его суммируемости, наз. тауборовыми условиями.
Условия, к-рые накладываются на ряд в этих случаях, помимо его суммируемости, наз. тауборовыми условиями.
Эти условия могут выражаться в различных формах. Наиболее распространенными для рядов (*) являются условия вида:
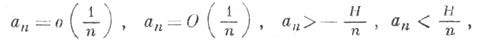 Н - постоянная,
Н - постоянная,
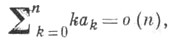
а также их обобщения, где натуральный параметр пзаменен переменным tn. В Т. т. к таким условиям, помимо приведенных выше, относятся, напр., следующие: если ряд (*) суммируем методом Бореля к сумме
Sи 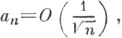 то ряд сходится к S.
то ряд сходится к S.
Для каждого регулярного матричного метода суммирования существуют числа 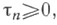 такие, что
такие, что 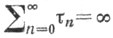 и условие
и условие 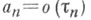 является тауберовым для этого метода (т. е. из суммируемости ряда этим методом и условия
является тауберовым для этого метода (т. е. из суммируемости ряда этим методом и условия 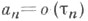 следует сходимость ряда).
следует сходимость ряда).
Тауберовы условия могут выражаться через оценки частичных сумм Sn ряда или оценки разности Sn-Sm при определенных соотношениях между пи т. Примерами Т. т. с такими условиями являются следующие: если ряд (*) с частичными суммами Sn суммируем методом Бореля к сумме Sи
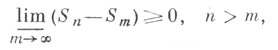
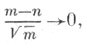 то ряд сходится к S;если ряд (*) суммируем методом Абеля к сумме Sи его частичные суммы Sn удовлетворяют условию Sn=0(1), то он суммируем к Sметодом Чезаро ( С,1).
то ряд сходится к S;если ряд (*) суммируем методом Абеля к сумме Sи его частичные суммы Sn удовлетворяют условию Sn=0(1), то он суммируем к Sметодом Чезаро ( С,1).
Тауберовьш условием может служить лакунарность ряда: а n=0 при п=п k условие в этом случае выражается через свойства последовательности {nk}.
Кроме обычной суммируемости, в теории суммирования рассматриваются Т. т. для специальных видов суммируемости (абсолютной, сильной, суммируемости со скоростью и др.).
Лит.:[1] Tauber A., лMonats. Math, und Physik

 Наиболее часто в теории суммирования рассматривается случай, когда метод Втождествен сходимости. В Т. т., относящихся к этим случаям, устанавливаются условия на ряд (последовательность), при к-рых из суммируемости ряда данным методом следует его сходимость. Назв. теорем восходит к А. Тауберу [1], впервые доказавшему две теоремы такого тина для Абеля метода суммирования:
Наиболее часто в теории суммирования рассматривается случай, когда метод Втождествен сходимости. В Т. т., относящихся к этим случаям, устанавливаются условия на ряд (последовательность), при к-рых из суммируемости ряда данным методом следует его сходимость. Назв. теорем восходит к А. Тауберу [1], впервые доказавшему две теоремы такого тина для Абеля метода суммирования: 
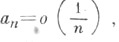 то ряд сходится к S;
то ряд сходится к S; 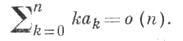
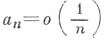 можно заменить на
можно заменить на 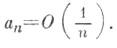 Условия, к-рые накладываются на ряд в этих случаях, помимо его суммируемости, наз. тауборовыми условиями.
Условия, к-рые накладываются на ряд в этих случаях, помимо его суммируемости, наз. тауборовыми условиями. 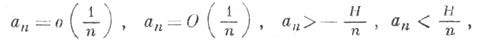 Н - постоянная,
Н - постоянная, 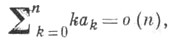
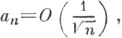 то ряд сходится к S.
то ряд сходится к S. 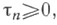 такие, что
такие, что 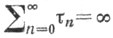 и условие
и условие 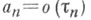 является тауберовым для этого метода (т. е. из суммируемости ряда этим методом и условия
является тауберовым для этого метода (т. е. из суммируемости ряда этим методом и условия 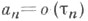 следует сходимость ряда).
следует сходимость ряда). 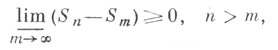
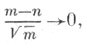 то ряд сходится к S;если ряд (*) суммируем методом Абеля к сумме Sи его частичные суммы Sn удовлетворяют условию Sn=0(1), то он суммируем к Sметодом Чезаро ( С,1).
то ряд сходится к S;если ряд (*) суммируем методом Абеля к сумме Sи его частичные суммы Sn удовлетворяют условию Sn=0(1), то он суммируем к Sметодом Чезаро ( С,1).