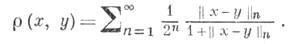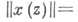|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЧЕТНОНОРМИРОВАННОЕ ПРОСТРАНСТВОЗначение СЧЕТНОНОРМИРОВАННОЕ ПРОСТРАНСТВО в математической энциклопедии: локально-выпуклое пространство X, топология к-рого задается с помощью счетной совокупности согласованных норм
Пример С. п.- пространство целых аналитических в единичном круге |z|<1 функций с топологией равномерной сходимости на любом замкнутом подмножестве этого круга и совокупностью норм Лит.:[1] Гельфанд И. М., Шилов Г. Е., Пространства основных и обобщенных функций, М., 1958. |
|
|
|

 т. е. таких, что если последовательность
т. е. таких, что если последовательность 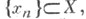 фундаментальная по нормам
фундаментальная по нормам  и
и  по одной из них сходится к нулю, то по второй также сходится к нулю. Последовательность норм
по одной из них сходится к нулю, то по второй также сходится к нулю. Последовательность норм  можно заменить неубывающей,
можно заменить неубывающей, 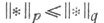 при p<q, порождающей ту же топологию с базой окрестностей нуля
при p<q, порождающей ту же топологию с базой окрестностей нуля 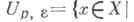
 С. н. метризуемо, и метрика может быть задана равенством
С. н. метризуемо, и метрика может быть задана равенством