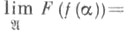"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СХОДИМОСТЬ
Значение СХОДИМОСТЬ в математической энциклопедии:
- одно из основных понятий математич. анализа, означающее, что нек-рый математич. объект имеет предел. В этом смысле говорят о С. последовательности каких-либо элементов, С. ряда, С. бесконечного произведения, С. цепной дроби, С. интеграла и т. п. Понятие С. возникает, напр., при изучении математич. объектов с помощью приближения их в каком-то смысле более простыми. Так. для вычисления площади круга используется последовательность площадей правильных многоугольников, вписанных в этот круг; для приближенных вычислений интегралов от функций применяются аппроксимации их кусочно линейными функциями или, более общо, сплайнами и т. п. Можно сказать, что математич. анализ начинается с того момента, когда в множестве тех или иных элементов введено понятие С.-
I. Сходимость последовательностей. В одном и том же множестве элементов можно вводить разные понятия С. его элементов в зависимости от изучаемого вопроса. Большую роль использование понятия С. играет при решении всевозможных уравнений (алгебраических, дифференциальных, интегральных и т. п.), в частности при нахождении их численных приближенных решений. Например, с помощью последовательных приближений метода можно получить последовательность функций, сходящихся к соответствующему решению данного обыкновенного дифференциального уравнения, и тем самым одновременно доказать при определенных условиях существование решения и дать метод, позволяющий вычислить это решение с нужной точностью. Как для обыкновенных дифференциальных уравнений, так в уравнений с частными производными существует теория различных сходящихся разностных методов их численного решения, удобных для их использования на современных вычислительных машинах.
Если в нек-ром множестве X введено понятие С. последовательностей его элементов, т. е. в совокупности всех указанных последовательностей выделен нек-рый класс, каждая последовательность к-рого названа сходящейся, и всякой сходящейся последовательности поставлен в соответствие нек-рый элемент из множества Х, наз. ее пределом, то само множество Хназ. пространством со сходимостью.
Обычно от понятия С. последовательностей требуется, чтобы оно обладало следующими свойствами:
1) каждая последовательность элементов множества Х может иметь не более одного предела;
2) всякая стационарная последовательность {х, х, . . . , х, . . .}, является сходящейся и ее пределом является элемент х;
является сходящейся и ее пределом является элемент х;
3) всякая подпоследовательность сходящейся последовательности также является сходящейся и имеет тот же предел, что и вся последовательность.
При выполнении этих условий пространство Xназ. часто пространством со сходимостью по Фреше. Примером такого пространства является всякое хаусдорфово топологич. пространство, а следовательно, любое метрич. пространство, в частности счетно-нормированное, а потому и просто нормированное (но отнюдь не всякое полунормированное) пространство. Для того чтобы последовательность сходилась в полном метрич. пространстве, необходимо и достаточно, чтобы она была фундаментальной.
Примером неметризуемого пространства со сходимостью по Фреше является пространство всех действительных функций, определенных на числовой оси  для к-рых С. последовательности
для к-рых С. последовательности  п=1, 2, . . . , означает ее С. при каждом фиксированном
п=1, 2, . . . , означает ее С. при каждом фиксированном 
Если в пространстве со сходимостью по Фреше Xопределить для каждого его подмножества  замыкание
замыкание  как совокупность всех точек пространства X, к-рые являются пределом последовательностей точек, принадлежащих множеству А, то пространство Xможет не оказаться топологич. пространством, т. к. не обязательно замыкание
как совокупность всех точек пространства X, к-рые являются пределом последовательностей точек, принадлежащих множеству А, то пространство Xможет не оказаться топологич. пространством, т. к. не обязательно замыкание  замыкания
замыкания  всякого множества Апри данном определении будет совпадать с
всякого множества Апри данном определении будет совпадать с 
Если в одном и том же множестве введены два определения С. и всякая последовательность, сходящаяся в смысле первого определения, сходится и в смысле второго, то говорят, что вторая сходимость сильнее первой. Во всяком пространство со С. Xможно ввести более сильную С. так, что порожденная ей операция замыкания превратит уже X в топологич. пространство, короче говоря, каждое пространство со С. может быть вложено в топологич. пространство, состоящее из тех же точек.
Во всяком топологич. пространстве определено понятие С. последовательностей его точек, но этого понятия недостаточно, вообще говоря, для того чтобы описать замыкание любого множества в этом пространстве, т. е. дать определение точек прикосновения множества, и, следовательно, недостаточно, чтобы полностью описать топологию данного пространства. Чтобы это стало возможно, вводится понятие сходящейся обобщенной последовательности .
Частично упорядоченное множество  наз. направленным множеством, если за любыми двумя его элементами имеется следующий за ними. Отображение
наз. направленным множеством, если за любыми двумя его элементами имеется следующий за ними. Отображение  направленного множества
направленного множества  в нек-рое множество Xназ. обобщенной последовательностью или направленностью в X. Обобщенная последовательность
в нек-рое множество Xназ. обобщенной последовательностью или направленностью в X. Обобщенная последовательность  в топологич. пространстве Xназ. сходящейся к точке х 0 из X, если для каждой окрестности Uточки х 0 существует такое
в топологич. пространстве Xназ. сходящейся к точке х 0 из X, если для каждой окрестности Uточки х 0 существует такое  что для всех
что для всех  выполняется включение
выполняется включение  В этом случае говорят, что предел обобщенной последовательности
В этом случае говорят, что предел обобщенной последовательности 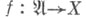 существует и равен х 0, при этом пишут
существует и равен х 0, при этом пишут 
В этих терминах замыкание множества, лежащего в топологич. пространстве X, описывается следующим образом: для того чтобы точка хпринадлежала замыканию 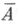 множества
множества 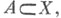 необходимо и достаточно, чтобы нек-рая обобщенная последовательность точек из Xсходилась к х;а для того чтобы топологич. пространство было хаусдорфовым, необходимо и достаточно, чтобы каждая обобщенная последовательность его точек имела не более одного предела.
необходимо и достаточно, чтобы нек-рая обобщенная последовательность точек из Xсходилась к х;а для того чтобы топологич. пространство было хаусдорфовым, необходимо и достаточно, чтобы каждая обобщенная последовательность его точек имела не более одного предела.
В терминах С. обобщенных последовательностей можно сформулировать и критерий непрерывности отображения Fтопологич. пространства Xв топологич. пространство Y: для непрерывности отображения Fв точке  необходимо и достаточно, чтобы для каждой обобщенной последовательности
необходимо и достаточно, чтобы для каждой обобщенной последовательности  такой, что
такой, что 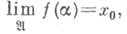 выполнялось бы условие
выполнялось бы условие 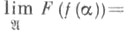

II. Сходимость числовых последовательностей и рядов.
Простейшим примером, иллюстрирующим понятие С., являются сходящиеся числовые последовательности, т. е. последовательности комплексных чисел {zn}, имеющие конечные пределы, и сходящиеся числовые ряды, т. <е. ряды, последовательности частичных сумм к-рых сходятся. Сходящиеся числовые последовательности и ряды часто применяются для получения различных оценок, а в численных методах - для приближенных вычислений значений функций и различных постоянных. В подобных задачах важно, с какой лскоростью

 является сходящейся и ее пределом является элемент х;
является сходящейся и ее пределом является элемент х;  для к-рых С. последовательности
для к-рых С. последовательности  п=1, 2, . . . , означает ее С. при каждом фиксированном
п=1, 2, . . . , означает ее С. при каждом фиксированном 
 замыкание
замыкание  как совокупность всех точек пространства X, к-рые являются пределом последовательностей точек, принадлежащих множеству А, то пространство Xможет не оказаться топологич. пространством, т. к. не обязательно замыкание
как совокупность всех точек пространства X, к-рые являются пределом последовательностей точек, принадлежащих множеству А, то пространство Xможет не оказаться топологич. пространством, т. к. не обязательно замыкание  замыкания
замыкания  всякого множества Апри данном определении будет совпадать с
всякого множества Апри данном определении будет совпадать с 
 наз. направленным множеством, если за любыми двумя его элементами имеется следующий за ними. Отображение
наз. направленным множеством, если за любыми двумя его элементами имеется следующий за ними. Отображение  направленного множества
направленного множества  в нек-рое множество Xназ. обобщенной последовательностью или направленностью в X. Обобщенная последовательность
в нек-рое множество Xназ. обобщенной последовательностью или направленностью в X. Обобщенная последовательность  в топологич. пространстве Xназ. сходящейся к точке х 0 из X, если для каждой окрестности Uточки х 0 существует такое
в топологич. пространстве Xназ. сходящейся к точке х 0 из X, если для каждой окрестности Uточки х 0 существует такое  что для всех
что для всех  выполняется включение
выполняется включение  В этом случае говорят, что предел обобщенной последовательности
В этом случае говорят, что предел обобщенной последовательности 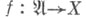 существует и равен х 0, при этом пишут
существует и равен х 0, при этом пишут 
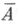 множества
множества 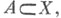 необходимо и достаточно, чтобы нек-рая обобщенная последовательность точек из Xсходилась к х;а для того чтобы топологич. пространство было хаусдорфовым, необходимо и достаточно, чтобы каждая обобщенная последовательность его точек имела не более одного предела.
необходимо и достаточно, чтобы нек-рая обобщенная последовательность точек из Xсходилась к х;а для того чтобы топологич. пространство было хаусдорфовым, необходимо и достаточно, чтобы каждая обобщенная последовательность его точек имела не более одного предела.  необходимо и достаточно, чтобы для каждой обобщенной последовательности
необходимо и достаточно, чтобы для каждой обобщенной последовательности  такой, что
такой, что 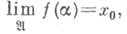 выполнялось бы условие
выполнялось бы условие