"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СХОДИМОСТИ МНОЖИТЕЛИЗначение СХОДИМОСТИ МНОЖИТЕЛИ в математической энциклопедии:
для функционального ряда 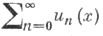 - числа - числа  п=0,1, 2, . . ., такие, что ряд п=0,1, 2, . . ., такие, что ряд 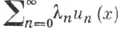 сходится почти всюду на измеримом множестве X, где и п (х) - числовые функции, определенные на X. сходится почти всюду на измеримом множестве X, где и п (х) - числовые функции, определенные на X.
Напр., для тригонометрич. ряда Фурье функции из L1 С. м. являются числа 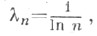 п=2, 3, ... п=2, 3, ...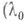 и и 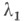 можно выбрать произвольно), то есть если можно выбрать произвольно), то есть если 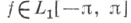 и и 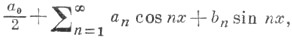
то ряд 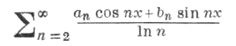
сходится почти всюду на всей числовой прямой. Если же 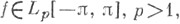 то ее тригонометрич. ряд Фурье уже сам" сходится почти всюду (см. Карлесона теорема). то ее тригонометрич. ряд Фурье уже сам" сходится почти всюду (см. Карлесона теорема).
Л. Ц. Кудрявцев.
|

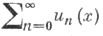 - числа
- числа  п=0,1, 2, . . ., такие, что ряд
п=0,1, 2, . . ., такие, что ряд 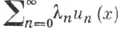 сходится почти всюду на измеримом множестве X, где и п (х) - числовые функции, определенные на X.
сходится почти всюду на измеримом множестве X, где и п (х) - числовые функции, определенные на X. 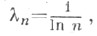 п=2, 3, ...
п=2, 3, ...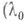 и
и 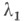 можно выбрать произвольно), то есть если
можно выбрать произвольно), то есть если 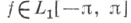 и
и 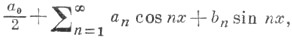
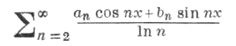
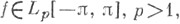 то ее тригонометрич. ряд Фурье уже сам" сходится почти всюду (см. Карлесона теорема).
то ее тригонометрич. ряд Фурье уже сам" сходится почти всюду (см. Карлесона теорема).